Формула Бернулли
ДО 5 баллов за конспект
ИСПЫТАНИЯ ПО СХЕМЕ БЕРНУЛЛИ
Формула Бернулли
Пусть одно за другим проводится n независимых одинаковых испытаний (экспериментов), причем каждый раз проверяется, произошло или нет некоторое событие А. Говорят еще, что если событие А произошло, то произошел “успех”, а если произошло событие 
, то случилась “неудача”. Считается, что вероятность “успеха” не меняется от испытания к испытанию. Ее обозначают как 
. Тогда и вероятность “неудачи” одна и та же во всех n испытаниях, она равна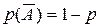 
и обозначается буквой q.
Элементарный исход всей такой серии из n экспериментов можно описать последовательностью из 
букв У или Н, буква У соответствует “успеху”, буква Н - неудаче. Всего, следовательно, 
элементарных исходов. Когда n = 3, то возможных исходов 8: УУУ; УУН; УНУ; УНН; НУУ; НУН; ННУ; ННН, где, например, исход УНУ означает, что “успех” произошел в первом и третьем экспериментах и не произошел во втором.
Испытания называются независимыми, если вероятность каждого элементарного исхода равна произведению соответствующих вероятностей “успеха” и “неудачи”, т. е. произведению чисел p и q.
Например, р(УУУ) = р3, р(УНУ) = р2q, р(УУН) = р2q, р(ННУ) = рq2, р(ННН) = q3и т.д.
Найдем вероятность события В = {в n независимых испытаниях “успех” произошел ровно k раз (0 £ k £ n)}. Событию В благоприятствуют все элементарные исходы, которые содержат k букв У ((n – k)букв Н соответственно). Вероятность любого такого исхода равна произведению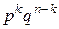 
, всего исходов столько, сколько есть разных последовательностей из букв У и Н, содержащих k букв У и (n – k) букв Н. Общее количество таких последовательностей равно 
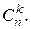Окончательно получаем:
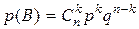. (6.1)
Эта формула называется формулой Бернулли, а вероятность р(В) обозначается рn(k). Вероятности рn(k) (0 £ k £ n) называют еще биноминальными, потому что произведение 
представляет собой общий член разложения бинома Ньютона
. (6.2)
Так как p + q = 1, то сразу получим, что сумма всех биноминальных вероятностей равна 1: 
.
6.2. Наивероятнейшее число появлений “успеха”