Действительные числа
Множество действительных чисел будем обозначать 
. Любое его подмножество называется числовым множеством. На множестве действительных чисел определены операции сложения и умножения:
· каждой паре действительных чисел 
и 
ставится в соответствие действительное число, называемое суммой и обозначаемое 
,
· каждой паре действительных чисел и ставится в соответствие действительное число, называемое произведением и обозначаемое 
. Символ 
в дальнейшем будет, как правило, опускаться.
Множество действительных чисел обладает следующими свойствами.
А. Операция сложения.
А1. 
А2. 
А3. Существует такое действительное число, называемое нулем и обозначаемое 
, что 
.
А4. Для любого действительного числа найдется такое действительное число , что 
. Число называют противоположным числом к числу и обозначают 
. Число 
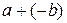называют разностью чисел и . При этом пишут 
. Тем самым определена операция вычитания.
B.Операция умножения.
B1.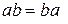 
B2. 
B3. Существует действительное число, называемое единицей и обозначаемое 1, что 
.
B4. Для любого действительного числа 
существует действительное число , что 
. Число называется обратным числом к числу и обозначается 
. Число 
называют отношением (частным) чисел и . Тем самым определена операция деления.
С. Связь операций сложения и умножения.
D.Упорядоченность.
На множестве действительных чисел определено отношение порядка. Для любых двух действительных чисел имеет место одно из двух соотношений:
либо 
(“ меньше ”), или, что то же самое, 
(“ больше ”),
либо 
, или, что то же самое, 
.
При этом выполняются следующие условия:
D1.Если и 
, то 
.
D2.Если , то 
.
D3.Если и 
, то 
.
Соотношения порядка называют также сравнением действительных чисел по величине, или неравенствами. Запись 
означает, что либо , либо 
.
Из свойств D2 - D3следует важное свойство множества действительных чисел, называемое плотностью действительных чисел: для любых двух различных действительных чисел и , ,найдется такое третье число 
, что 
.
E. Непрерывность множества действительных чисел.
Для любых числовых множеств 
и 
таких, что любая пара чисел 
и 
стеснена неравенством 
, существует такое число 
, что 
.
Перечисленные свойства полностью определяют множество действительных чисел
Важные подмножества действительных чисел
1. Числа 1,2,3,… называются натуральными числами. Множество натуральных чисел будем обозначать 
.
2. Множество 
называется множеством целых чисел. Очевидно, 
3.Множество 
называется множеством рациональных чисел. Очевидно, 
.
4. Множество 
– дополнение множества рациональных чисел до множества действительных чисел, называется множеством иррациональных чисел.
5. Пусть и – два действительных числа, . Выделяют следующие типы числовых множеств, называемые числовыми промежутками:
– отрезок,
– интервал,
– полуинтервалы.
Определение.Числовое множество называют ограниченным сверху, если существует такое число 
, что для всех 
имеет место неравенство 
. Число называют в этом случае числом, ограничивающим сверху множество .
Пример.Промежуток 
является примером ограниченного сверху множества. В качестве числа , ограничивающего сверху это множество, может быть выбрано любое неотрицательное число.
Определение.Числовое множество называют ограниченным снизу, если существует такое число 
, что для всех имеет место неравенство 
. Число называют в этом случае числом, ограничивающим снизу множество .
Пример.Промежуток 
является примером ограниченного снизу множества. В качестве числа , ограничивающего снизу это множество, может быть выбрано любое неположительное число.
Определение. Числовое множество называют ограниченным, если оно ограничено сверху и снизу.
Пример 1.Интервал 
является ограниченным множеством, поскольку он ограничен сверху и снизу. Действительно, в качестве числа , ограничивающего снизу это множество может быть выбрано, например, число 
, а в качестве числа, ограничивающего множество сверху, выступает, например, число 
.
Пример 2.Промежуток 
является ограниченным снизу и неограниченным сверху числовым множеством. Промежуток является примером ограниченного сверху, но неограниченного снизу числового множества.
Определение 1.Есличисловое множество ограничено сверху, то наименьшее из чисел, ограничивающих сверху множество , называют его верхней гранью и обозначают
, или 
(от латинского слова supremum – наибольший).
Определение 2.Есличисловое множество ограничено снизу, то наибольшее из чисел, ограничивающих снизу множество, называют его нижней гранью и обозначают
, или 
(от латинского слова infinum – наименьший).
Приведенные выше содержательные определения верхней и нижней граней числовых множеств могут быть переформулированы и даны в строгой математической форме.
Определение 1*.Число
называется верхней гранью числового множества , если
1. для любого выполняется неравенство 
;
2. для любого числа 
существует число , что 
.
Определение 2*.Число
называется нижней гранью числового множества , если
1. для любого выполняется неравенство 
;
2. для любого числа 
существует число , что 
.
Пример 1. Рассмотрим множество 
. Оно является ограниченным. Не трудно убедиться, что среди всех чисел, ограничивающих сверху это множество, наименьшим является число 2, а из всех чисел, ограничивающих множество снизу, наибольшим является число –1. Таким образом,
.
Заметим, что если точная грань множества достигается на этом множестве, т.е принадлежит рассматриваемому множеству, то вместо 
и 
пишут 
и 
соответственно.
Пример 2. Рассмотрим полуинтервал [0,4). Не трудно видеть, что 
, причем здесь 
, 
, т.е. нижняя грань принадлежит множеству, а верхняя грань ему не принадлежит. В этом случае мы вправе написать 
.