Примеры решения задач

Пример 1. Если прямые а, b, с принадлежат одному пучку прямых, то имеем: Sc× S × S = S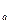d , где Sd - осевая симметрия относительно некоторой четвертой прямой, принадлежащей тому же пучку.

Докажем это. Пусть а, b, с принадлежат одному пучку.

1. Пусть .

Тогда S × S 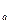- есть поворот вокруг точки О на угол 2a (a - угол между прямыми а и b). Поворот вокруг точки О на угол 2a может быть представлен через композицию двух других осевых симметрий, оси которых также пересекаются в точке О под углом a.

Пусть осью одной из таких симметрий является прямая с, а другой некоторая прямая d. Т.к. композиции S × S 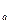и Sd× Sc представляют собой один и тот же поворот, то имеет место равенство композиций

S ×S 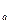= Sd× Sc.

На основании свойства композиции преобразований “умножив” обе части этого равенства на Sc, получим: Sc× S × S 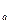= Sd .

2. Прямые a, b, c – параллельны между собой.

Тогда S ×S 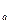- есть параллельный перенос Т 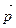, где вектор 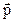перпендикулярен прямым а и b, расстояние между прямыми а и b равно , и направление от первой прямой до второй совпадает с направлением вектора 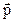. Параллельный перенос на вектор 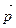может быть представлен через композицию двух других осевых симметрий, оси которых также параллельны.

Пусть осью одной из таких симметрий является прямая с, а другой некоторая прямая d.

Т.к. композиции S × S 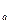и Sc× Sd представляют собой один и тот же параллельны перенос, то имеет место равенство композиций

S ×S 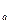= Sc× Sd .

На основании свойства композиций преобразований “умножив” обе части этого равенства справа на Sc, получим:

S × S 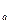× Sc = Sd ,

где d – прямая, параллельная прямой с, и при этом расстояние между прямыми с и d равно ,а направление от первой прямой до второй совпадает с направлением вектора .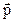

 

Пример 2. Доказать, что произведение двух центральных симметрий есть параллельный перенос.

Решение: Пусть Z1 - отражение от точки О1 и Z2 - отражение от точки О2. Т.к. Z1 и Z2 - движения первого рода, то Z2×Z1 - движение первого рода. Рассмотрим два возможных случая.

1)Точки О1 и О2 совпадают. В этом случае, очевидно, Z2×Z1– тождественное преобразование, т.е. параллельный перенос на нулевой вектор.

2) Точки О1 и О2 не совпадают. При движении Z2×Z1 образы О1' и О2' точек О1 и О2 лежат на прямой О1О2, и кроме того, точка О2 является серединой отрезка О1О1',

а точка О1 – серединой отрезка О О . .

Поэтому прямая О1О2 является инвариантной прямой преобразования Z2×Z1. На этой прямой нет ни одной неподвижной точки. Если, например, А - неподвижная точка, то О1А = О1'А, т.е. А совпадает с точкой О2, что невозможно, т.к. О2 не является неподвижной точкой. Итак, Z2×Z1 – движение первого рода, которое имеет инвариантную прямую, на которой нет неподвижных точек. Отсюда следует, что Z2×Z1 – параллельный перенос на ненулевой вектор 2 .

 

Пример 3. Найти преобразование, которое является произведением центральной симметрии Z0 и осевой симметрии Sp.

Решение. Т.к. Zo - движение первого рода, а Sp - движение второго рода, то SpZ0 - движение второго рода, т.е. либо осевая симметрия, либо скользящая симметрия.

Рассмотрим первый случай: О Î р. Тогда заменяя центральную симметрию произведением двух осевых, оси которых перпендикулярны, и при этом выбирая одну из них прямую р, а в качестве другой возьмем прямую s, проходящую через точку О перпендикулярно р, получим

SpZ0 = Sр× Sр× Ss = Ss – осевая симметрия.

Пусть O Ï р. Тогда заменяем центральную симметрию произведением двух осевых, оси которых перпендикулярны, и при этом выбирая одну из них прямую g, параллельную прямой р, а в качестве другой возьмем прямую s, проходящую через точку О перпендикулярно р, получим

SpZ0 = Sр× Sg× Ss = ×Ss – скользящая симметрия, так как

|| р.

Пример 4. Докажите, что композиция параллельного переноса и центральной симметрии (в обоих порядках) является центральной симметрией.

Доказательство. Имеем f = ZO T 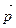. Разложим данные преобразования в произведение осевых симметрий:

f= S4 S3 S2 S1 ,

где Si – определяется прямой аi.

Прямые а1||а2, а2||а3, прямая а4 им перпендикулярна. Прямые а2 и а3 можно совместить, за счет сдвига прямых, определяющих параллельный перенос. При этом получим новую прямую . В результате

f= S4 S1’ = ZA,

так как прямые и а4 перпендикулярны, при этом А – точка пересечения этих же прямых ( см.теорема 9 § 6) .

 

Пример 5.Докажите, что если точку отразить симметрично относительно точек О1, О2 и О3, а затем ещё раз отразить симметрично относительно этих же точек, то она вернется на место. Согласно примера 2 имеем:

Поэтому, – тождественное преобразование, так как вектор параллельного переноса равен нулевому вектору.

Пример 6. Доказать, что композиция поворотов вокруг вершин углов треугольника АВС соответственно на углы А, В, С этого треугольника есть центральная симметрия.

Решение. Мы выбираем треугольник АВС и считаем порядок следования его вершин по часовой стрелке. Для нахождения композиции трех поворотов сначала найдем композицию двух поворотов, а затем композицию полученного поворота и поворота вокруг третьей вершины. Каждый раз, вычисляя композицию двух поворотов, следует выбирать оси симметрии так, чтобы одна из них была общей.

Пусть f= RC · RB · RA. Обозначим О – центр вписанной окружности в треугольник АВС. Тогда

RB · RA = S(OB) ·S(AB) ·S(AB) ·S(OA) =

= S(OB) ·S(OA) = R = S(OC) ·Sm.

Прямая m определяется условиями:

О Î m,

Ð (m, (OC)) = ).

Так как

) = = ,

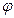и угол при вершине О в треугольнике ТОС равен 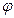, где Т точка касания вписанной окружности в треугольник АВС со стороной AC, то прямая m совпадает с прямой ОТ.

Обратим внимание на то, что

(ОТ) ^ (АС).

Рассмотрим:

f= RC · RB · RA = f= RC · S(OC) ·Sm =

= S(AC) · S(OC) ·S(OC) ·S(OT) =

= S(AC) · S(OT) = ZT .

Таким образом, f = ZT .

 

Пример 7. Построить квадрат, две противоположные вершины которого лежат на данной прямой l, а две другие – соответственно на данных окружностях