Аксиомы, определяющие вероятность
· Каждому случайному событию А ставят в соответствие некоторое неотрицательное число, называемое его вероятностью: 0≤p(А)≤1
· Аксиома сложения. Для несовместимых событий справедливо высказывание: «Вероятность суммы событий равна сумме вероятностей этих событий»: p(А1+А2+…+Аn)=p(A1)+p(A2)+…+p(An)
· Для произвольных событий существует теорема сложения: p(A+B)=p(A)+p(B)-p(AB)
· Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного появления
· Если А‹В, то вероятность события А не может превысить вероятность В.
· Для любого А: p (А) – вероятность противоположного события: p(Ā)=1-p(A).
Кроме двух требований к системе может быть предъявлено третье требование, а именно: если элементами системы являются события А1, А2, …,Аn, то в систему входит их сумма и произведение. Такое поле событий называется борелевским (1847-1956).
Случайные события подчиняются следующим законам:
· Коммутативный:
A+B=B+A;

A∙B=B∙A.

· Ассоциативный:
A+(B+C)=(A+B)+C

A(BC)=(AB)C
 →
→ 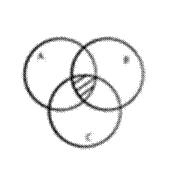 =
=
 →
→ 
· Дистрибутивный :
A(B+C)=AB+AC
 →
→ 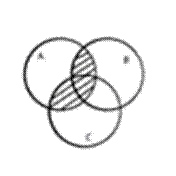 =
=
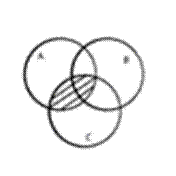 +
+  →
→ 
A+(BC)=(A+B)(A+C)
 →
→  =
=
 +
+ 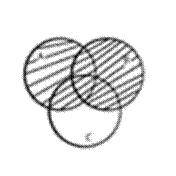 →
→ 