ГЕТЕРОГЕННЫЕ РАВНОВЕСИЯ.

Федеральное агентство по рыболовству

ФГОУ ВПО «Астраханский государственный технический университет»

 

Кафедра «Органическая, биологическая и физколлоидная химия» (ОРХ)

 

 

Методические указания к лабораторному

Практикуму по теме

“Фазовые диаграммы”

Лабораторная работа №17

«Построение диаграммы растворимости системы вода-фенол»

 

 

АСТРАХАНЬ 2007 г.

 

АВТОРЫ:кандидат химических наук, доцент кафедры органической , биологической и физколлоидной химии Стороженко Валентина Николаевна; кандидат химических наук, доцент кафедры органической биологической и физколлоидной химии Летичевская Наталья Николаевна; кандидат химических наук, доцент кафедры органической биологической и физколлоидной химии

Пащенко Константин Петрович

 

 

Методические указания рассмотрены и одобрены на заседании кафедры органической, биологической и физколлоидной химии 25.06.07г. протокол №7

 

РЕЦЕНЗЕНТ: кандидат химических наук, доцент кафедры органической биологической и физколлоидной химии Шинкарь Елена Владимировна.

ВВЕДЕНИЕ

Термический анализ занимается изучением равновесных диаграмм «состав-свойство», в которых в качестве свойства берется температура. Методика работы сводится к получению кривых нагревания и охлаждения чистых веществ и их смесей, на основании которых строится общая диаграмма системы.

Изучением различных систем занимается раздел химии, называемый физико-химическим анализом. Физико-химический анализ изучает соотношение между составом и свойствами в однокомпонентных, двух- и многокомпонентных средах.

При пространственном изображении диаграммы двухкомпонентной системы пользуются прямоугольной системой координат, на одной оси откладывают температуру Т, на другой — давление Р, на третьей — концентрацию С. Существование каждой фазы системы изображается вполне определенным объемом в пространстве координат. Для практических целей часто пользуются диаграммами «состав-свойство».

ГЕТЕРОГЕННЫЕ РАВНОВЕСИЯ.

Система, состояние которой не изменяется во времени, причем эта неизменность не обусловлена внешними процессами, находится в термодинамическом равновесии. Обычно это равновесие является динамическим, т. к. в системе процессы идут в противоположном направлении и результаты их взаимно уничтожаются. Примером может служить равновесие между водой и паром. В единицу времени обмен молекулами между жидкой фазой и парообразной одинаков: т.е. число молекул, уходящих из жидкости в пар равно количеству молекул приходящих из пара в жидкость. Поэтому с кинетической точки зрения термодинамическое равновесие характеризуется как подвижное. Система, способная обмениваться энергией с окружающей средой остается неизменной до тех пор, пока внешние условия остаются постоянными.

Гомогенной системой называется такая однородная система, которая во всех своих частях обладает одними и теми же физическими и химическими свойствами и не имеет видимых поверхностей раздела. Например: раствор, смесь газов индивидуальное твердое вещество и т.д.

Гетерогенной системой является неоднородная система, внутри которой имеются поверхности раздела, отделяющие друг от друга части системы, различающиеся по свойствам. Например: вода и лед, насыщенный раствор соли и кристаллы соли и т.д.

Фазой называется гомогенная часть гетерогенной системы, химический состав и все физические свойства которой одинаковы. Например: смесь воды со льдом представляет собой две фазы, вода - одну фазу, лед - другую.

Таким образом, гомогенная система состоит из одной фазы, а гетерогенная - из нескольких фаз.

Индивидуальные вещества, наименьшее число которых достаточно для образования всех фаз, являются компонентами. Число компонентов в

системе, в которой не может идти химическая реакция, равно числу составляющих ее индивидуальных веществ. Число компонентов в системе, в которой могут идти химические реакции, равно числу образующих ее индивидуальных веществ минус число независимых химических реакций. Для пояснения рассмотрим следующие случаи:

1. В системе КNО₃ и NаNO₃ оба индивидуальных вещества являются компонентами, т.к. в этой системе химическая реакция не протекает, и количества составляющих веществ можем менять независимо один от другого.

2. В системе, образованной из воды, хлористого калия, хлористого магния, сульфата калия и сульфата магния имеется пять индивидуальных веществ, но компонентов будет четыре, так как в ней может происходить следующая химическая реакция:

2КСl+МgSО₄→МgСl₂+К₂ SО₄

3. В системе, образованной из аммиака, хлористого аммония и хлористого водорода в общем случае будут два компонента, т. к. возможна реакция

NH₄Cl→HCl+NH₃

и поэтому число компонентов равно: З - 1 = 2. т.е. для построения двухфазной системы нам достаточно двух веществ. При диссоциации твердого хлористого аммония образуются эквимолярные количества газообразных NH₃ и НСl.

Если в рассматриваемую систему внести второе условие [NH₃] = [НСl], то число компонентов уменьшается до единицы (3 – 2= 1).

Таким образом, при этих условиях обе фазы системы (твердая и

газообразная) могут быть образованы из одного компонента — хлористого аммония.

В зависимости от числа компонентов системы различаются на однокомпонентные, двухкомпонентные и т.д.

Величины, характеризующие состояние системы, называются термодинамическими параметрами, например: давление, температура, концентрация, внутренняя энергия, энтропия и т.д. Термодинамические параметры фаз системы, находящейся в равновесии, которым можно придавать произвольные значения в том интервале, при котором число фаз не изменяется, являются термодинамическими степенями свободы.

В системе, находящейся в состоянии термодинамического равновесия, зависимость между числом степеней свободы, числом компонентов и числом фаз дается уравнением правила фаз, или, точнее, законом равновесия фаз. Допустим, что имеется равновесная система, которая состоит из К-компонентов и Ф-фаз, и пусть состояние каждой фазы будет определено: температура Т, давление Р, и состав, т.е. концентрация веществ, находящихся в фазе. Для определения состава каждой фазы из К-компонентов нужно знать процентное содержание или мольные доли (К - 1) компонентов, а для определения состава Ф-фаз нужно знать процентное содержание Ф (К - 1) компонентов. Для полной характеристики системы нужно знать Ф (К - 1) + 2 переменных. Т.к. наша система находится в состоянии термодинамического равновесия, то не все переменные Ф (К - 1) + 2 являются независимыми. При равновесии каждый компонент так распределяется в различных фазах, что химический потенциал (μ) его будет одним и тем же во всех фазах. Обозначая нумерацию фаз верхними индексами (I, II, III ... Ф), а нумерацию компонентов нижними индексами 1, 2, 3 ... К) можно составить еще (Ф - 1 )К уравнений.

μ₁^I=μ₁^II=μ₁^III=…=μ₁^Ф

μ₂^I=μ₂^II=μ₂^III=…=μ₂^Ф

μ₃^I=μ₃^II=μ₃^III=…=μ₃^Ф

μ_k^I=μ_k^II=μ_k^III=…=μ_k^Ф

Каждая строка дает Ф-1 уравнений и т.к. количества строк равно К, то, следовательно, всех уравнений имеется К (Ф-1).

Так как число всех переменных, характеризующих состояние, равно Ф (К - 1) + 2, а условием равновесия связаны (Ф - 1) К переменных, то число независимых переменных “С” будет равно:

С=[Ф(К-1)+2]-(Ф-1)К

С=ФК-Ф-ФК+К+2

С=К-Ф+2

Это уравнение называется правилом фаз Гиббса или уравнением равновесия. “С” - число термодинамических степеней свободы. Оно показывает максимальное количество переменных, величина которых может изменяться независимо одна от другой. Число степеней свободы может быть только положительным.

Пользуясь уравнением равновесия фаз, можно классифицировать разнообразные системы по числу компонентов, по числу фаз и по числу степеней свободы. В зависимости от числа степеней свободы системы разделяются на инвариантные, когда не имеется ни одной степени свободы, моновариантные, когда имеется одна степень свободы, дивариантные, когда имеется две степени свободы и т.д. В качестве примера рассмотрим однокомпонентную систему - воду. Если имеем одну фазу, например, пар, то в этом состоянии система имеет две степени свободы, т.к. состояние газа характеризуется тремя переменными: температурой Т, давлением Р и объемом V, но из них только две являются независимыми, т.к. уравнение состояния РV = nRT связывает их с третьей. При равновесии воды с паром в системе имеется одна степень свободы, т.е. в данном случае каждому значению давления будет соответствовать одно определенное значение температуры. В случае равновесия между льдом, водой и паром в системе не имеется ни одной степени свободы, т.к. это состояние строго характеризуется определенными значениями температуры и давления (Р = 6,1 гПа Т 0,0076°С). На рис.1 приведена диаграмма состояния воды в области средних давлений. Три кривые разбивают диаграмму на поля, каждое из которых отвечает одному из агрегатных состояний воды — пару, жидкости и льду. Кривая отвечает равновесию между соответствующими двумя фазами. Кривая ОС характеризует зависимость давления насыщенного пара жидкой воды от температуры и называется кривой испарения; кривая ОВ — зависимость температуры замерзания воды от внешнего давления и называется кривой плавления; кривая ОА — зависимость давления насыщенного пара льда от температуры и называется кривой возгонки. Точка О выражает условие одновременного равновесия между паром, льдом и жидкой воды. Кривая OD определяет давление насыщенного пара над переохлажденной водой.

 

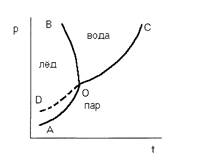
рис.1