Фазовая манипуляция (ФМн).

При фазовой манипуляции, являющейся частным случаем квадратурной манипуляции, информационным параметром является фаза сигнала-носителя информации, которая изменяется скачкообразно под действием модулирующего сигнала. На практике фазовая манипуляция используется при небольшом числе возможных значений начальной фазы - как правило, 2, 4 или 8, т.е. в современных цифровых каналах связи применяются двоичная, 4-уровневая и 8-уровневая ФМн.

При этом при приеме сигнала сложно измерить абсолютное значение начальной фазы в посылках; значительно проще определить относительный фазовый сдвиг между двумя соседними символами. Кроме того, из-за случайных искажений радиосигнала может иметь место неопределенность фазы восстановленной несущей, что является причиной, так называемой, обратной работы, при которой двоичные посылки принимаются за "негатив".

Для устранения этих явлений обычно применяется разностное кодирование фазы передаваемых радиоимпульсов, т.е. определяется относительный фазовый сдвиг в соседних посылках. Такую манипуляцию фазы называют фазоразностной или относительной фазовой манипуляцией (ОФМн). Таким образом, в цифровых каналах связи с ОФМн при передаче информации кодируется не сама фаза радиосигнала, а разность фаз (фазовый сдвиг) двух соседних радиоимпульсов. Этот метод обеспечивает по сравнению с частотной манипуляцией (ЧМн) выигрыш по полосе более чем в 2 раза, при равной скорости передачи информации вдвое большая помехоустойчивость, чем у ЧМн и вчетверо большая, чем у амплитудной манипуляции (AМн); при равной помехоустойчивости в канале с белым шумом в 4 раза более высокая скорость по сравнению с ЧМн. Правило кодирования при ОФМн приведено на рис. 5.

 

Рис. 5.

 

Здесь:	Переход:	1 → 1	- скачок фазы
		1 → 0	- нет скачка фазы
		0 → 0	- нет скачка фазы
		0 → 1	- скачок фазы

 

При двоичной ОФМн длительность радиоимпульса τ = Т. В случае многоуровневой манипуляции (N > 2) исходная последовательность двоичных элементов длительностью Т с помощью кодера модулятора преобразуется в совокупность двух (при N = 4) или трех (при N = 8) последовательностей двоичных элементов длительностью τ = 2Т (при N = 4) или τ = 3Т (при N = 8).

Комбинация двоичных элементов получаемых последовательностей используются при кодировании фазового сдвига при ОФМн. При ОФМн при передаче логической «1» фаза несущего колебания скачком изменяется на Δφ, например, на π, по отношению к фазе предыдущего бита, а при передаче логического «0» – фаза остается той же, что и у предыдущего бита. Например, при 4-уровневом ОФМн, фазовый сдвиг кодируется следующим образом:

 

Символ первой последовательности
Символ второй последовательности
Фазовый сдвиг		π/2	π	3π/2

 

Чаще применяется четырехфазнаяОФМн (ОФМн-4), или двукратнаяОФМн (ДОФМн), основанная на передаче четырех сигналов, каждый из которых несет информацию о двух битах (ди-бите) исходной двоичной последовательности. Обычно используется два набора фаз: в зависимости от значения ди-бита (00, 01, 10 или 11) фаза сигнала может измениться на 0°, 90°, 180°, 270° или 45°, 135°, 225°, 315° соответственно. При этом, если число кодируемых бит более трех (8 позиций поворота фазы), резко снижается помехоустойчивость ОФМн. По этой причине для высокоскоростной передачи данных ОФМн не используется.

При демодуляции фаза ОФМн радиосигнала сравнивается с фазой восстановленного на приемном конце опорного колебания (несущей). Применяются два способа демодуляции ОФМн радиосигналов. В первом случае сначала восстанавливается сигнал несущей частоты и одновременно детектируется ОФМн радиосигнал, затем разностно (диффференциально) декодируются принимаемые сигналы. Второй способ предполагает дифференциально - когерентное (автокорреляционное) детектирование ОФМн радиосигнала, при котором в качестве опорного колебания используется предшествующий радиоимпульс. При этом операция детектирования и декодирования совмещены.

 

2.7. Амплитудно-фазовая манипуляция (АФМн).

При АФМн изменяется как фаза, так и амплитуда сигнала, что позволяет увеличить количество кодируемых бит и при этом существенно повысить помехоустойчивость. Другими словами, изменяющимся параметром в данном методе является комплексная амплитуда радиосигнала. Применение многоуровневой АФМн позволяет обеспечить высокую эффективность использования полосы частот. Формирование М-уровневого АФМн радиосигнала может быть реализовано путем М - уровневой балансной амплитудной манипуляции квадратурных колебаний одной частоты и сложение полученных амплитудно - модулированных радиосигналов. По этой причине АФМ часто называют квадратурной амплитудной манипуляцией (КАМн). Наиболее распространена 16-уровневая АФМн или КАМн-16.

В настоящее время используются способы модуляции, в которых число кодируемых на одном бодовом интервале информационных бит может достигать 8...9, а число позиций сигнала в сигнальном пространстве - 256...512.

Квадратурное представление сигналов является удобным и достаточно универсальным средством их описания. Квадратурное представление заключается в выражении колебания линейной комбинацией двух ортогональных составляющих - синусоидальной и косинусоидальной, т.е. каждому из возможных значений дискретного символа C_k ставится в соответствие пара величин - амплитуды т.н. синфазной и квадратурной составляющих либо, что эквивалентно, амплитуда и начальная фаза несущего колебания:

 

C_k ® (a_k, b_k), s(t) = a_k cos w₀t + b_k sin w₀t, t < (k + 1)T,

или

C_k ® (A_k, j _k), s(t) = A_k cos(w₀t + j _k), t < (k + 1)T.

 

Параметры аналогового колебания, сопоставленные дискретному символу C_k, удобно представлять в виде комплексного числа в алгебраической (a_k + jb_k) или экспоненциальной (A_k exp(jj _k)) форме. Совокупность этих комплексных чисел для всех возможных значений дискретного символа называется сигнальным созвездием.

Такая дискретная модуляция (манипуляция) осуществляется по двум каналам на несущих, сдвинутых на 90° друг относительно друга, т.е. находящихся в квадратуре (отсюда и название представления и метода формирования сигналов).

Поясним работу квадратурной схемы (рис. 6) на примере формирования сигналов четырехфазной ОФМн (ФМ-4).

 

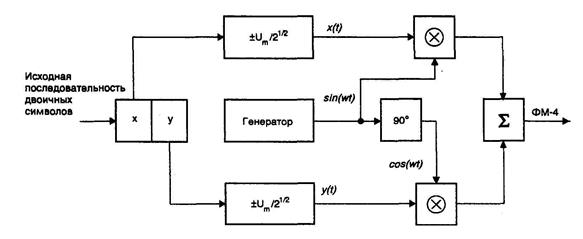
Рис. 6

 

Исходная последовательность двоичных символов длительностью Т при помощи регистра сдвига разделяется на нечетные импульсы, которые подаются в квадратурный канал (cos(w₀t)), и четные, поступающие в синфазный канал (sin(w₀t)). Обе последовательности импульсов поступают на входы соответствующих формирователей манипулирующих импульсов, на выходах которых образуются последовательности биполярных импульсов a_k и b_k. Импульсы a_k и b_k поступают на входы канальных перемножителей, на выходах которых формируются двухфазные (0,π) ФМ колебания. После суммирования они образуют сигнал ФМ-4. В соответствии с методом формирования сигнал ФМ-4 также называют квадратурным ФМ сигналом.

При одновременной смене символов в обоих каналах модулятора (с 10 на 01, или с 00 на 11) в сигнале ОФМн происходит скачок фазы на 180°.

Такие скачки фазы, также имеющие место и при обыкновенной двухфазной модуляции (ФМ-2), вызывают паразитную амплитудную модуляцию огибающей сигнала. В результате этого при прохождении сигнала через узкополосный фильтр возникают провалы огибающей до нуля (рис. 7). Такие изменения сигнала нежелательны, поскольку приводят к увеличению энергии боковых полос и помех в канале связи.

 

Рис. 7.

 

ЧетырехфазнаяФМ со сдвигом (рис. 8) позволяет избежать скачков фазы на 180° и, следовательно, глубокой модуляции огибающей. Формирование сигнала в квадратурной схеме происходит так же, как и в модуляторе ФМ-4 (рассмотренном выше). Единственным отличием является то, что манипуляционные элементы информационной последовательности x(t) и y(t) смещены во времени на длительность одного элемента Т, как показано на рис. 8, б, в.

Изменение фазы при таком смещении модулирующих потоков определяется лишь одним элементом последовательности, а не двумя, как при ФМ-4. В результате скачки фазы на 180^о отсутствуют, так как каждый элемент последовательности, поступающий на вход модулятора синфазного или квадратурного канала, может вызвать изменение фазы на 0°, +90° или -90°.

 

Рис. 8.

 

Демодулируется сигнал с квадратурной манипуляцией так же, как и в случае аналоговой квадратурной модуляции - сигнал умножается на два несущих колебания, сдвинутых по фазе друг относительно друга на 90°, а результаты умножения пропускаются через фильтр низких частот (ФНЧ). На выходе этих ФНЧ будут получены аналоговые сигналы синфазной и квадратурной составляющих. Далее эти сигналы дискретизируются с частотой, равной символьной скорости.

Пары отсчетов синфазной и квадратурной составляющих образуют комплексное число, и ближайшая к этому числу точка используемого созвездия (а точнее - соответствующий этой точке информационный символ) выдается в качестве выходного результата.