ПЕРИОДИЧЕСКИЙ НЕГАРМОНИЧЕСКИЙ СИГНАЛ

Математическая модель периодического сигнала – периодическая функция времени x(t) с периодом Т=2p/w₁, удовлетворяющая условиям Дирихле (ограниченная, кусочно-непрерывная, с конечным числом экстремумов и точек разрыва первого рода на протяжении периода).

Приняв множество в качестве базисной системы (полной системы ортогональных функций в произвольном интервале (t_0,t₀+T) при любых t₀ ) получим обобщённую математическую модель периодического сигнала - ряд Фурье в тригонометрической форме:

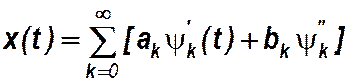
Коэффициенты ряда - и .

При k=0 получим 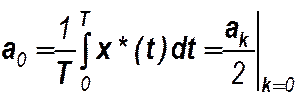и

(характерная структура мат. модели для чётных и нечётных сигналов: пределы интегр-ния)

Если ввести обозначения a_k=A_kCosj_k и b_k=A_kSinj_k, отдельное слагаемое в обобщённой мат. модели приводится к виду, соответствующему модели гармонического сигнала:

a_kCoskw₁t + b_kSinkw₁t = A_k(Coskw₁t Cosj_k+ Sinkw₁t Sinj_k) = A_kCos(kw₁t-j_k).

Подставим его в обобщённую математическую модель периодического сигнала. Согласно приведенным формулам коэффициентов ряда Фурье при k=0, b₀=A₀Sinj₀=0, что возможно только при j₀=0; отсюда a₀=A₀Cosj₀ = A₀Cos0 =A₀.С учётом этого получим другой вид тригонометрической модели периодического сигнала:

Она свидетельствует, что периодический сигнал включает постоянную составляющую A₀ и бесконечно большое число гармонических сигналов, называемых гармониками. Гармоника с k=1 и частотой w₁=2p/T,совпадающей с частотой периодического сигнала, называется основной гармоникой. Остальные составляющие с k >1 и частотами w_k=kw₁,кратными основной частоте, называют высшими гармониками. Амплитуды и начальные фазы гармоник определяются по коэффициентам ряда:

и