Образец выполнения типового задания

1. Строим простой возрастающий вариационный ряд:

12, 13, 14, 15, 16, 17, 18.

2. Рассчитываем простое среднее арифметическое:

N

X =	∑хi i=1	=	12+13+14+15+16+17+18	=		=15
N

3. Вычисляем среднее квадратическое отклонение:

при N≤ 30,	S =	√	N ∑ di2 i=1
N-1

где d_i – является разностью между i-той вариантой ряда (х_i) и средним арифметическим (X): d_i = х_i – X̄, N – общее количество вариант.

S =	√	∑ (xi - X)2 i=1	=

 

=	√	(12-15)2 +(13-15)2 + (14-15)2 + (15-15)2 + (16-15)2 + (17-15)2 + (18-15)2	= 2,16

 

4. Рассчитываем ошибку среднего арифметического:

при N≤30	µ X =	S	=	2,16	=	2,16	= 0,88
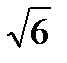
		2,45

5. Вычисляем доверительный интервал с использованием таблицы значений критерия Стьюдента (таблица 3.1).

5.1. При α = 0,05 (5%) ⇒γ = 95% и числе наблюдений N = 7,

критерий T= t_y = 2,4, тогда: ∆ = Т*µ = 2,4 ∙ 0,88 = 2,11

Таким образом, доверительные интервалы средней величины

(X-Δ и X+Δ): X = 15 + 2,11 или средняя частота дыханий в минуту колеблется от 12,89 до 17,11 ⇒X =[ 12,89; 17,11].

5.2. При α = 0,01 (5%) ⇒γ = 99% и числе наблюдений N = 7,

критерий T= t_y = 3,7, тогда: ∆ = Т*µ = = 3,7 ∙ 0,88 = 3,26

Следовательно, доверительные интервалы средней величины -

X = 15 ± 3,26 или средняя частота дыханий в минуту колеблется от 11,74 до 18,26 ⇒X =[ 11,74; 18,26].