Центральная предельная теорема
При изучении нормального закона распределения отмечают, что непрерывная случайная величина формируется под воздействием очень большого числа независимых случайных факторов. Причем сила воздействия каждого отдельного фактора мала и не может превалировать среди остальных, а характер воздействия - аддитивный (т. е. при воздействии случайного фактора F на величину а получается величина а + D(F), где случайная “добавка” D(F) мала и равновероятна по знаку).
Центральная предельная теорема устанавливает условия образования в пределе нормального закона распределения. Она была открыта Лапласом[8] (опубликована в 1812 г.). Состоит она в следующем.
Рассмотрим сумму S = 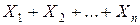 независимых случайных величин. Предположим, что все эти случайные величины имеют одинаковое распределение и принимают целочисленные значения 0; ±1; ±2; ... Распределение
независимых случайных величин. Предположим, что все эти случайные величины имеют одинаковое распределение и принимают целочисленные значения 0; ±1; ±2; ... Распределение 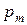 = P(
= P(  ) каждой из величин
) каждой из величин  можно изобразить следующим образом. Нарисуем на каждом значении m прямоугольник, середина основания которого есть точка m, длина основания равна 1,0, а площадь есть
можно изобразить следующим образом. Нарисуем на каждом значении m прямоугольник, середина основания которого есть точка m, длина основания равна 1,0, а площадь есть 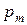 . Получится ряд прямоугольников (с высотами
. Получится ряд прямоугольников (с высотами 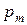 ), сумма площадей которых равна 1 (рис. 5.1).
), сумма площадей которых равна 1 (рис. 5.1).

Рис. 5.1
Попытаемся изобразить таким же образом вероятности отдельных значений суммы  =
= 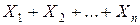 при довольно большом числе n. При этом обнаружим, что даже если случайные величины
при довольно большом числе n. При этом обнаружим, что даже если случайные величины  , i = 1, ... , n принимали всего лишь два значения 0 и 1, то значениями суммы
, i = 1, ... , n принимали всего лишь два значения 0 и 1, то значениями суммы  могут быть числа от 0 до n. Следовательно, эти значения при большом числе n просто не поместятся в прежнем масштабе на рис. 5.1. Мы вынуждены будем изменить масштаб, т. е. вместо значений случайной величины
могут быть числа от 0 до n. Следовательно, эти значения при большом числе n просто не поместятся в прежнем масштабе на рис. 5.1. Мы вынуждены будем изменить масштаб, т. е. вместо значений случайной величины
 =
= 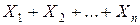
будем откладывать значения величины
 =
=  (
(  -
-  ),
),
где  и
и  – некоторые числа, зависящие от n.
– некоторые числа, зависящие от n.
Лаплас открыл, что получится нечто замечательное, если положить
 = M(
= M( 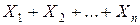 ) = nа, где а = M(
) = nа, где а = M(  );
);
 =
=  =
=  , где
, где  = D(
= D(  ).
).
Случайную величину

мы будем называть нормированной суммой.
Очевидно, что M(  ) = 0, D(
) = 0, D(  ) = 1 и значениями величины
) = 1 и значениями величины  являются числа
являются числа
 =
=  ,
,
причем для любого целого m
P(  = m) =P(
= m) =P(  =
=  ) = P(
) = P(  =
=  ).
).
Отложим по оси абсцисс значения  и изобразим вероятности
и изобразим вероятности
P(  =
=  )
)
этих значений прямоугольниками, середины оснований которых лежат в точках  , длины оснований равны расстоянию
, длины оснований равны расстоянию
 -
-  =
= 
между соседними точками, а площади равны P(  =
=  ). Высоты этих прямоугольников равны
). Высоты этих прямоугольников равны
 ∙ P(
∙ P(  =
=  ).
).
При этом произойдет следующее: верхние основания этих прямоугольников почти точно лягут на некоторую кривую, задаваемую уравнением
f(x) = 
 ,
,
которое является плотностью нормального распределения.
При  имеем
имеем
 P(
P(  =
=  ) ®
) ® 
 .
.
В таком случае нам известно, что
P(a 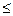

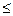 b) » F (b) – F (a).
b) » F (b) – F (a).
Рассмотрим общую часть центральной предельной теоремы в любой ее форме. Пусть  , … – последовательность независимых случайных величин с математическими ожиданиями M(
, … – последовательность независимых случайных величин с математическими ожиданиями M(  ) и дисперсиями D(
) и дисперсиями D(  ) =
) =  ,
,  , … . Введем новые случайные величины:
, … . Введем новые случайные величины:
 =
= 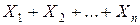 ,
,
для которых
M(  ) =
) =  ; D(
; D(  ) =
) =  ; σ(
; σ(  ) =
) =  .
.
Тогда при определенных условияхсправедливо равенство
 P(½
P(½  ½< z) =
½< z) = 
 = 0,5 + F(
= 0,5 + F(  ),
),
утверждающее, что закон распределения нормированных отклонений суммы  при
при  стремится к стандартному нормальному распределению вне зависимостиот типа распределения слагаемых. В таком случае говорят, что
стремится к стандартному нормальному распределению вне зависимостиот типа распределения слагаемых. В таком случае говорят, что  подчиняется асимптотически нормальному распределению.
подчиняется асимптотически нормальному распределению.
Различные формы центральной предельной теоремы отличаются друг от друга ограничениями, налагаемыми на последовательность  , при которых выполняется утверждение теоремы. Так, в теореме Муавра[9]–Лапласа
, при которых выполняется утверждение теоремы. Так, в теореме Муавра[9]–Лапласа
в качестве  рассматриваются частоты при i-том испытании в модели Бернулли. Более общим является условие одинакового распределения всех
рассматриваются частоты при i-том испытании в модели Бернулли. Более общим является условие одинакового распределения всех  при существовании конечного математического ожидания M(
при существовании конечного математического ожидания M(  ) = a и дисперсии D(
) = a и дисперсии D(  ) =
) =  .
.
А. М. Ляпунов[10], создав специальный метод характеристических функций, используемый в доказательстве различных предельных теорем, показал, что требование одинакового распределения  можно заменить условием их равномерной малости (удельный вес каждого отдельного слагаемого
можно заменить условием их равномерной малости (удельный вес каждого отдельного слагаемого  должен стремиться к нулю при увеличении числа слагаемых). Это условие Ляпунова математически выражается так:
должен стремиться к нулю при увеличении числа слагаемых). Это условие Ляпунова математически выражается так:

 = 0, где аi = M½
= 0, где аi = M½  – M(
– M(  )½3.
)½3.