Предельные теоремы теории вероятностей

Лекция №

 

Рассмотрим ряд утверждений и теорем из большой группы так называемых предельных теорем ТВ, устанавливающих связь между теоретическими и экспериментальными характеристиками СВ при большом числе испытаний над ними. Они составляют основу математической статистики. Предельные теоремы условно делят на две большие группы. Первая группа теорем, называемая законом больших чисел (ЗБЧ), устанавливает устойчивость средних значений: при большом числе испытаний их средний результат перестает быть случайным и может быть предсказан с достаточной точностью. Вторая группа теорем, называемая центральной предельной теоремой (ЦПТ), устанавливает условия, при которых закон распределения суммы большого числа СВ неограниченно приближается к нормальному.

Начнем с рассмотрение неравенства Чебышева, которое можно использовать для грубой оценки вероятностей событий, связанных со СВ, распределение которых неизвестно, а также для доказательства ряда теорем ЗБЧ.

Неравенство Чебышева (1-я форма). 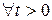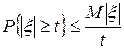или, что эквивалентно, .

Доказательство приведем для НСВ с плотностью распределения .

Неравенство Чебышева (2-я форма). Если существует , то или .

Доказательство: используя первую форму неравенства Чебышева, получаем:

Неравенство Чебышева в таком виде устанавливает верхнюю границу вероятности события, а в виде - нижнюю границу.

 

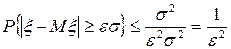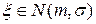Пусть , где . Тогда по неравенству Чебышева (2-я форма) имеем: . В частности при или . Получили так называемое «правило трех сигм», согласно которому с практической достоверностью (с вероятностью ) множество возможных значений любой СВ, обладающей дисперсией, есть интервал . Напомним, что для СВ эта вероятность равна 0,9973.

Неравенство Чебышева справедливо для любых СВ. Рассмотрим некоторые частные случаи:

1) для СВ , , распределенной по биномиальному закону, неравенство Чебышева примет вид: , т.к. , ;

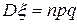2) для частости (относительной частоты) события в n независимых испытаниях, в каждом из которых оно может произойти с вероятностью , дисперсия которых , неравенство Чебышева принимает вид: ;

3) пусть 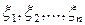- независимые СВ, имеющие математическое ожидание и дисперсию . Пусть СВ . Тогда , 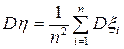. Неравенство Чебышева для СВ 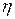имеет вид:

или . (1)

Пример 1

Вероятность наличия опечатки на одной странице рукописи равна 0,2. Оценить вероятность того, что в рукописи, содержащей 400 страниц, частость появления опечатки отличается от соответствующей вероятности по модулю меньше, чем на 0,05.

Воспользуемся неравенством Чебышева:

.

 

Основное утверждение ЗБЧ содержится в теореме Чебышева. В ней и других теоремах ЗБЧ используется понятие «сходимости СВ по вероятности».

Определение

СВ сходятся по вероятности к величине А (случайной или неслучайной) если вероятность события при стремится к единице, т.е. .

ЗБЧ в форме Чебышева. Если СВ независимы и их дисперсии ограничены сверху одним и тем же числом , т.е. , , то

,

т.е. среднее арифметическое этих СВ сходится по вероятности к среднему арифметическому их математических ожиданий.

Доказательство: согласно неравенству Чебышева (1) при , получаем

.

Переходя к пределу при и учитывая, что вероятность любого события не превышает 1, получаем

.

Теорема Чебышева подтверждает связь между случайностью и необходимостью: СВ практически не отличается от неслучайной величины .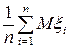

Следствие

Пусть независимые и одинаково распределенные СВ с математическим ожиданием и конечной дисперсией , , то

,

т.е. среднее арифметическое СВ сходится по вероятности к математическому ожиданию а.

 

Пример 2

Глубина моря измеряется прибором, не имеющим систематической ошибки. Среднее квадратическое отклонение измерений не превосходит 15 м. Сколько нужно сделать независимых измерений, чтобы с вероятностью, не меньшей 0,9, можно было утверждать, что среднее арифметическое этих измерений отличается от а (глубины моря) по модулю меньше, чем на 5 м?

 

Обозначим через 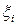, 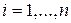результаты n независимых измерений глубины моря. Необходимо найти число n, которое удовлетворяет неравенству

,

где , что означает отсутствие при измерениях систематической ошибки (т.е. измерения производятся с одинаковой точностью). По условию , 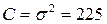. Отсюда

,

т.е. , . Измерение нужно проводить не менее 90 раз.

 

Теорема Бернулли исторически является первой и наиболее простой формой ЗБЧ. Она теоретически обосновывает свойство устойчивости относительной частоты.

 

ЗБЧ в форме Бернулли. Если вероятность появления события A в одном испытании равна p, число наступления этого события при n независимых испытаниях равно , то для любого числа имеет место равенство

,

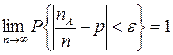т.е. относительная частота 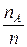события А сходится по вероятности к вероятности p появления события А в одном испытании.

Доказательство

Введем в рассмотрение случайные величины 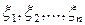следующим образом: 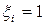, если в i-ом испытании появилось событие А, а если не появилось, то 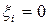. Закон распределения СВ 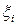, 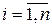имеет вид:

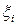
Р	1-p	p

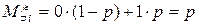
Таким образом, СВ 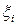независимы, их дисперсии ограничены одним и тем же числом , т.к.

.

Поэтому к этим СВ можно применить теорему Чебышева:

.

Так как и , то .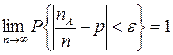

Теорема Бернулли теоретически обосновывает возможность приближенного вычисления вероятности события с помощью его относительной частоты.

Обобщением теоремы Бернулли на случай, когда вероятности появления события А в каждом из n испытаний различны, является теорема Пуассона:

,

где - вероятность события A в i-ом испытании.