Формирование желаемой логарифмической амплитудной частотной характеристики
Метод логарифмичеких частотных характеристик вследствие его эффективности и наглядности является наиболее распространенным среди аналитических методов синтеза корректирующих устройств. В реализации этого метода можно выделить несколько этапов:
– первый – состоит в формировании желаемой логарифмической амплитудной частотной характеристики. Желаемой называют такую логарифмическую амплитудную частотную характе ристику (ЛАЧХ), которая удовлетворяет требованиям, предъявляемым к проектируемой системе;
– второй – заключается в построении ЛАЧХ по передаточной функции исходной системы;
– на третьем этапе сопоставляются ЛАЧХ желаемой и исходной систем, на основании чего строится ЛАЧХ корректирующего устройства;
– на последнем этапе, как правило, методом математического моделирования, проверяется устойчивость скорректированной системы и её соответствие требуемым показателям качества.
Одним из показателей качества работы системы автоматического управления является точность воспроизведения входного задающего (управляющего) воздействия в установившемся режиме работы. Этот показатель оценивают по величине ошибки (отклонению регулируемой координаты от требуемого значения), которую можно подсчитать, используя теорему о конечном значении функции (§ 5.2 формулы (5.3) и (5.8)) или коэффициенты ошибок (5.14).
Частотный метод синтеза предполагает, что на систему подается гармонический управляющий сигнал, параметры которого известны:
, (7.1)
где gm – амплитуда и ωp – частота считаются рабочими. В том случае, когда параметры гармонического входного воздействия не известны, приводятся максимальные значения скорости и ускорения, требуемые от проектируемой системы. Для вращательного движения это будут угловая скорость α׳max и угловое ускорение α״max. В случае поступательного движения производится пересчет линейных скоростей и ускорений в угловые через параметры преобразователей (шарико-винтовой; винт-гайка; рейка-шестерня,
различные кривошипно-шатунные механизмы и т.д. и т.п.).
При заданных максимальных скорости – α׳max и ускорении – α״max используя (7.1), рассчитаем параметры эквивалентного гар-монического закона входного воздействия полагая:
(7.2)
(7.3)
Поделив (7.3) на (7.2), получим:
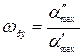– эквивалентную рабочую частоту; (7.4)
Возведя в квадрат обе части (7.2) и поделив его на (7.3), получим:
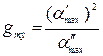– эквивалентную амплитуду воздействия. (7.5)
Полученные числовые значения используются для расчета параметров желаемой ЛАЧХ.
Исходя из требуемой ошибки амплитудой εm, по формуле (5.7) рассчитаем необходимый минимальный коэффициент передачи разомкнутой системы, который она должна иметь на рабочей
частоте.
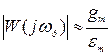. (7.6)
В логарифмических координатах амплитуды и частоты определяем местонахождение рабочей точки А, координаты которой: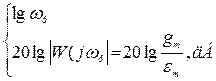 
(7.7)
Для астатических систем 1-го порядка строят запретную область, в которой не должна располагаться желаемая ЛАЧХ. Через рабочую точку проводят две прямые: в область низких частот с наклоном –1, а в сторону высоких частот с наклоном –2 (рис.7.1). Обос-нование построения запретной области дано в Приложении 5.
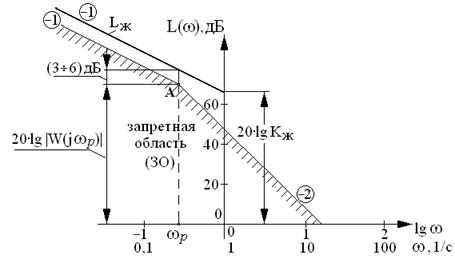
Рис.7.1
Динамические показатели качества системы управления зависят от наклона и протяженности среднечастотной асимптоты, проходящей через частоту среза. Известно [4,5,6 и др.], что частота среза и время регулирования связаны обратно пропорциональной зависимостью. Предлагаются различные способы определения частоты среза [5 ÷ 11], через которую затем проводится среднечастотная асимптота. Казалось бы, чем выше частота среза, тем меньше время регулирования. Но у этого требования есть и негативная сторона. Поскольку все элементы имеют ограниченную полосу пропускания, то высокочастотные сигналы для них будут помехой, нарушающей их тепловой режим работы. Например, механическая часть электродвигателя – исполнительного элемента системы, не сможет поворачиваться на требуемый угол, отрабатывая высокочастотный входной сигнал. А в то же самое время ток в цепи управления отреагирует на высокочастотный сигнал. В этом случае часть энергии пойдет на ненужный нагрев электродвигателя, что приведет к нарушению теплового баланса.
Асимптота в области средних частот проводится только с наклоном –1. Проведение асимптоты с наклоном –2 приводит к ситуации, когда система становится неустойчивой или близка к
границе устойчивости.
Протяженность среднечастотной асимптоты рекомендуется делать не менее декады, распределяя примерно равные отрезки по обе стороны от частоты среза. На практике эту асимптоту ограни-чивают сверху значениями амплитуды на уровне (12 ÷ 16) дБ и снизу – на уровне –(12 ÷ 16) дБ рис 7.2.
Рис.7.2
Две асимптоты одинакового –1-го наклона низкочастотную и среднечастотную сопрягают асимптотой, имеющей наклон –2 (реже с наклоном –3). Точки пересечения сопрягающей асимптоты определяют частоты сопряжения желаемой ЛАЧХ и, следовательно, постоянные времени (Т1 = 1/ω1 и Т2 = 1/ω2) передаточной функции желаемой системы (рис.7.3). Из точки пересечения среднечастотной асимптоты с уровнем –(12 ÷ 16) дБ проводится асимптота с наклоном –2 или –3. Частота излома на выбранном отрицательном уровне ЛАЧХ определяет постоянную времени Т3 = =1/ω3. Так как высокочастотная часть желаемой ЛАЧХ мало влияет на показатели качества, то при её построении руководствуются простотой реализации корректирующего устройства. Если выполняется условие 
, то влиянием звеньев,
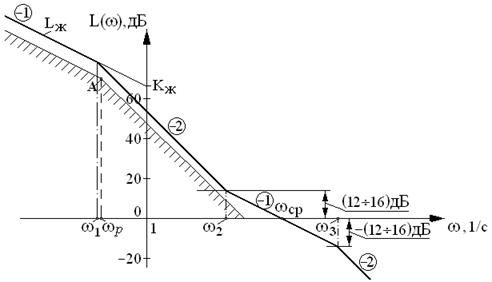
Рис.7.3
имеющих частоты сопряжения ωi, можно пренебречь.
Передаточная функция желаемой системы записывается по параметрам желаемой ЛАЧХ и имеет вид:
(7.8)
Далее при синтезе корректирующих устройств эта передаточная функция уточняется в соответствии с высокочастотной частью ЛАЧХ нескорректированной системы.
Изложим пошаговый способ построения желаемой ЛАЧХ.
После определения координат рабочей точки с учетом поправки на 3 ÷ 6 дБ проводится низкочастотная асимптота с наклоном –1. Эта прямая на частоте равной 1 определяет коэффициент усиления желаемой системы КЖ. Запишем в логарифмических координатах уравнение прямой низкочастотной асимптоты:
, дБ (7.9)
Так как точка с координатами (ω =1 с–1; КЖ, дБ) принадлежит прямой (7.9), то легко определяется Lа. Свободный член (7.9) Lа можно определять по параметрам рабочей точки или любой точки, принадлежащей низкочастотной асимптоте:
.
Подставляя Lа в (7.9), получим уравнение низкочастотной асимптоты:
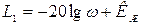(7.10)
Примем, что первый излом желаемой ЛАЧХ происходит на рабочей частоте, где коэффициент передачи равен L(ωp) = Lp. В этом случае первая частота сопряжения желаемой ЛАЧХ совпадает с рабочей частотой, что является необязательным условием (см. рис.7.3). Тогда точка с координатами (ωр ; Lp) принадлежит также и второй асимптоте с наклоном –2, уравнение которой в общем виде: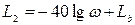 
.
Считая начальными условиями для построения второй асимптоты координаты первого излома ЛАЧХ (ωр ; Lp ), найдем свободный член Lb: 
. Окончательно уравнение 2-ой асимптоты будет:
(7.11)
Прямая (7.11), в свою очередь, имеет общую точку со среднечастотной асимптотой. Эта точка принадлежит второй частоте излома – ω2 . Если принять из рекомендуемого диапазона (12 ÷ 16 дБ) значение амлитуды на этой частоте, например L(ω2) = 16 дБ, , то можно, используя (7.11), рассчитать числовое значение ω2 и далее Т2 =1/ ω2.
и тогда
Далее запишем уравнение среднечастотной асимптоты, начальными значениями для которой могут служить частота ω2 и L(ω2):
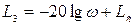
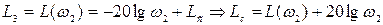
Окончательно уравнение среднечастотной асимптоты примет вид:
(7.12)
Частота ω3, определяющая постоянную времени Т3, рассчитывается по (7.12), исходя из выбранного уровня (–12 ÷ –16) дБ амплитуды, на котором происходит переход среднечастотной части желаемой ЛАЧХ к высокочастотной (с –1 наклона на –2 наклон).
Уравнение (7.12) среднечастотной асимптоты позволяет при необходимости вычислить значение частоты среза.
Приведем числовые примеры построения желаемой ЛАЧХ.
Пример 1.
Построить желаемую ЛАЧХ и записать её передаточную
функцию по следующим данным:
– закон входного воздействия 
;
– установившаяся ошибка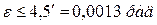 
;
– коэффициент перерегулирования 
;
– время регулирования при допуске 
tр ≤ 0,2 с.
Решение. Определим минимальный коэффициент передачи на рабочей частоте ωр=0,6 с–1.
С учетом поправки, которую принимаем равной 4дБ, коэффициент передачи на рабочей частоте будет равен 
(1995,3). По уравнению (7.9) (с начальными условиями ωр=0,6 с–1 ; L1=66 дБ) определяем его свободный член.
Уравнение первой низкочастотной асимптоты
(7.13)
позволит вычислить коэффициент усиления желаемой системы – Lж (Кж, дБ), определяемый на частоте ω=1с–1. Используя (7.13), получим 
. В безразмерных единицах Кж = 1196,7. Округляем Кж =1197.
Считая, что рабочая точка принадлежит также и 2-ой асимптоте, получим её уравнение (7.11).
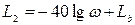. Приняв L2=Lp, а ω = ωр, получим 
Уравнение 2-ой асимптоты окончательно выглядит:
. Это уравнение используется для вычисления второй сопрягающей частоты ω2, задавшись значением уровня, с которого строится среднечастотная асимптота. Принимаем значение уровня равным 12 дБ, которое и подставляем в последнее равенство.
. Искомая частота ω2 = 13,44 с–1. Соответствующая этой частоте постоянная времени Т2 = 1/ω2 = 0,074 с.
Получим уравнение среднечастотной асимптоты, используя начальные условия: L(ω2)= 12 дБ
дБ.
Тогда окончательно уравнение среднечастотной асимптоты при-мет вид: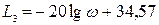 
.
Из последнего равенства допуская, что среднечастотная аси-мптота претерпевает излом на уровне –12 дБ, вычислим третью частоту сопряжения.
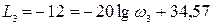. Из последнего равенства определяется частота ω3 = 213,1 с–1. По полученным результатам расчета:
Кж= 1197 (61,56 дБ); Т1= 1,67 с.; Т2 = 0,074 с.; Т3 = 0,0047 с. записываем первое приближение передаточной функции желаемой системы:
(7.14)
По (7.14) строится желаемая ЛАЧХ (рис.7.4) и моделированием проверяются динамические показатели качества (рис.7.5)
Рис.7.4
Рис.7.5
Полученные результаты: σ = 16,6% <20%; tp = 0,145 с < 0,2 c. дают основание продолжить синтез корректирующего устройства.
Пример 2. Сформировать желаемую ЛАЧХ по следующим данным:
– максимальная скорость объекта управления – α׳ = 1,2рад/с;
– максимальное ускорение объекта управления – α״ = 0,3 рад/с2 ;
– установившаяся ошибка при гармоническом управляющем воздействии – εm ≤ 0,0026 рад.;
– коэффициент перерегулирования σ ≤20%;
– время регулирования при допуске tp ≤ 0,16 c.
Решение. Рассчитаем параметры эквивалентного входного воздействия.
Рабочая частота 
;
Амплитуда 
Определяем координаты рабочей точки:
После введения поправки на 4 дБ и округления в большую сторону принимаем следующие координаты рабочей точки:
. (7.15)
Запишем уравнение 1-ой низкочастотной асимптоты
. (7.16)
Свободный член La определим, используя координаты рабочей точки, принадлежащей этой асимптоте.
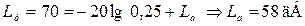
Подставив в уравнение (7.16) ω =1 с–1и La = 58 дБ, определяем Кж.
Кж = 58 дБ (Кж = 794).
Уравнение 2-ой асимптоты, проводимой с наклоном –2:
Считая рабочую точку, принадлежащей также и второй асимптоте, определяем свободный член Lb и уравнение принимает окончательный вид:
. (7.17)
Уравнение (7.17) позволяет определить значение 2-ой частоты излома, на которой аплитуду принимаем равной 12 дБ.
12 
.
Уравнение среднечастотной асимптоты:
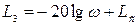
Свободный член Lс определяется из условия L3 = 12 дБ на частоте 
. 
. Тогда уравнение среднечастотной асимптоты окончательно примет вид:
. (7.18)
Равенство (7.18) позволяет рассчитать частоту ω3 третьего излома желаемой ЛАЧХ, если положить L3= –12дБ:
.
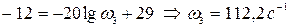По рассчитанным частотам сопряжения определяем соответствующие им постоянные времени:
По построенной желаемой ЛАЧХ (рис.7.6 , ЛАЧХ 1) записываем
Рис.7.6
её передаточную функцию:
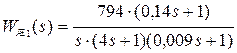, которую используем при моделировании для оценки динамических показателей качества. Математическое моделирование в программном комплексе МВТУ[1] дало (рис.7.7) следующие результаты: σ = 17% (hmax1 = 1,17), tp1= 0,27 c.
Сопоставляя полученные результаты с требуемыми значениями, можно увидеть, что время регулирования больше (tp1= 0,27 c > 0,16 c). Необходимо внести поправки. Оставаясь на первой асимптоте, сместим рабочую точку на частоту ω = 0,4 с–1. Выполнив расчеты по методике предыдущего примера, получим частоты сопряжения (ω1 = 0,4 с–1; ω2 = 8,95 с–1; ω3= 141,9 с–1), используя которые построим ЛАЧХ 2 и запишем передаточную функцию:
.
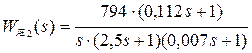Проверка динамических показателей путем математического моделирования дала следующие результаты (рис.7.7): σ = 16,6%
(hmax2 = 1,166), tp2 = 0,216 c. Следует отметить, что смещение рабо-
Рис.7.7
чей точки с целью снижения времени регулирования правильное, но недостаточное. Опять оставаясь на первой асимптоте, сместим рабочую точку на частоту ω = 0,8 с–1. По принятой методике и известным уравнениям получим новые частоты сопряжения (ω1 = = 0,8 с–1; ω2 = 12,68 с–1; ω3= 200,9 с–1), используя которые строится
ЛАЧХ 3 (рис. 7.6) и записывается передаточная функция:
(7.19)
Математическое моделирование дает следующие результаты (рис.7.7): σ = 16 % (hmax3 = 1,16), tp3 = 0, 15 c. Таким образом, ЛАЧХ 3 и соответствующая ей передаточная функция (7.19) удовлетворяет требованиям по показателям качества.
Если переходная функция имеет больший, чем требуется коэффициент перерегулирования, то необходимо увеличивать длину среднечастотной асимптоты сначала в область высоких частот.
Контрольные вопросы
1. Что понимается под определениями желаемая передаточ-
ная функция, желаемая ЛАЧХ?
2.Каким основным требованиям должна удовлетворять же-
лаемая ЛАЧХ? Перечислите динамические показатели ка-
чества.
3. Поясните содержание основных этапов формирования же
лаемой ЛАЧХ.
1. В отсутствие заданного гармонического закона входного
воздействия, как рассчитать эквивалентный ему закон и
какие данные для этого требуются?
2. Какими координатами определяется местонахождение ра-
бочей точки?
6. С каким наклоном проводится низкочастотная асимптота
в системе 1-го порядка астатизма?
7. Как строится запретная область?
8. Как определяется коэффициент усиления желаемой систе-
мы в децибелах и безразмерных единицах?
9. Какому из показателей качества должно удовлетворять ра-
сположение низкочастотной асимптоты желаемой ЛАЧХ?
10. С каким наклоном проводится среднечастотная асимпто-
та желаемой ЛАЧХ?
11.За какие показатели качества «отвечает» среднечастотная
асимптота?
12.Какой параметр среднечастотной асимптоты влияет на
перерегулирование?
13.На какой показатель качества и как влияет частота среза желаемой ЛАЧХ?
14. Чем руководствуются при формировании желаемой ЛАЧХ в области высоких частот?
15. В чем заключается пошаговый метод построения желаемой ЛАЧХ?