Тема 2.6. Связанные колебательные контуры

Занятие 2.6.1. Связанные колебательные контуры

Вопросы:

1. Схемы связанных контуров, коэффициент связи.

2. Схемы замещения, вносимые сопротивления.

3. Настройка связанных контуров.

4. Резонансные частоты связанных контуров.

Недостатком одиночных контуров (ПСКК и ПРКК) является недостаточная избирательность. АЧХ, по форме наиболее близкую к прямоугольной, могут обеспечить связанные колебательные контуры.

Связанный колебательный контур (СВКК) – это два и более одиночных контуров, связанных между собой общим магнитным или электрическим полем.

Контур, на который подается входное напряжение называют первичным. Контур, с которого снимают напряжение – вторичный. Бывают следующие виды СВКК:

- индуктивная связь:

- РИСУНОК –трансформаторная связь

- РИСУНОК – автотрансформаторная связь

- емкостная связь:

- РИСУНОК – внутриемкостная связь

- РИСУНОК – внешенеемкостная связь

Коэффициент связи

Свойства связанных контуров очень сильно зависят от степени связи между первичным и вторичным контуром. Для оценки этой связи введено понятие коэффициента связи. Изобразим обобщенную схему связанных контуров:

РИСУНОК

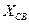- реактивное сопротивление элемента связи

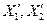- реактивные сопротивления контуров равноименные сопротивлению связи

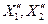- реактивные сопротивления контуров разноименные сопротивлению связи

Под коэффициентом трансформации из первичного контура во вторичный понимают отношение

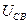- напряжение на элементе связи

- напряжение между элементами первичного контура

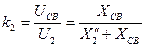
Коэффициент связи – среднее геометрическое из коэффициентов трансформации

Для трансформаторной связи коэффициент трансформации

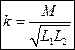
Для внутриемкостной связи

Коэффициент связи можно изменять от 0 до 1. Если значение коэффициента , то связь очень слабая

- слабая

- связь сильная

 

Для анализа связанных контуров целесообразно перейти от принципиальных схем к эквивалентной одноконтурной схеме. Вначале рассмотрим такой вариант:

РИСУНОК

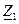- собственное сопротивление первичного контура

- собственное сопротивление вторичного контура

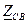- сопротивление элемента связи

Выбираем направления контурных токов, составляем систему уравнений:

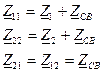
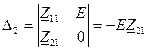
РИСУНОК

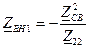- вносимое в первичный контур сопротивление из вторичного контура. Вносимое сопротивление учитывает влияние вторичного контура на первичный контур.

Вносимое сопротивление комплексное, в нем можно выделить вещественную и мнимую часть. Например, для трансформаторной связи

Графики вносимых сопротивлений имеют следующий вид, в зависимости от обобщенной растройки:

РИСУНОК

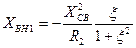- для одинаковых контуров

На самом деле, никто сопротивление из второго контура в первый не перемещает. Вносимое сопротивление характеризует ту энергию, которой обменивается первый контур со вторым и наоборот. характеризует безвозвратно ушедшую во второй контур энергию и потраченную там виде тепла. Видно, что максимально при нулевой расстройке (на резонансной частоте), уменьшается с расстройкой второго контура. Кроме того, увеличивается с увеличением коэффициента связи.

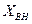характеризует энергию, которой обмениваются контуры друг с другом. Важно следующие, что 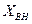противоположно по знаку реактивному сопротивлению второго контура, т.е. на тех частотах, где вторичный контур имеет индуктивный характер, активное сопротивление емкостное и наоборот. на резонансной частоте и имеет экстремумы еще на двух частотах. Это предполагает наличие двух дополнительных резонансных частот.

 

Настройка связанных контуров выполняется с целью получения максимально возможного тока в последним контуре.

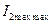
Имеется 3 органа настройки:

При этом 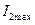, но не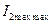

При этом 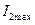, но не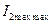

Сложный резонанс:

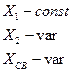или

Полный резонанс

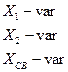
Настройка производится следующим образом: устанавливается минимальная связь, изменяются элементы , , добиваясь максимума тока во втором контуре, затем подстраивается 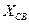, затем процесс повторяется несколько раз, т.к. если настроить в резонанс первый контур, а затем изменить , то изменяется и первый контур расстраивается, поэтому весь процесс повторяется многократно.

Резонансные частоты связанных контуров

Изобразим графически зависимость от обобщенной растройки

РИСУНОК

При достаточно сильной связи, реактивное сопротивление первого контура становится равным 0 на грех частотах. Графически, зависимость резонансных частот от коэффициента связи выглядит следующим образом:

РИСУНОК

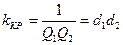
- для идентичных контуров

СВКК продолжение

1. Частотные характеристики СВКК

2. Средства улучшения избирательности СВКК

Под комплексным коэффициентом передачи понимают отношение

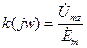
Вид АЧХ в значительной мере определяется коэффициентом связи.

РИСУНОК

1.

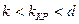
2.

3.

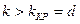
При связи меньше критической, вносимое реактивное сопротивление из вторичного контура меньше, чем собственное реактивное сопротивление первичного контура. Результирующее реактивное сопротивление

не достигает нулевого значения.

При коэффициенте связи больше критического, вносимое реактивное сопротивление увеличивается, результирующее реактивное сопротивление становится равным 0 еще на двух частотах. В центре появляется провал АЧХ. Это объясняется тем, что при увеличении связи возрастает активное вносимое сопротивление.

При дальнейшем изменении коэффициента связи расстояние между резонансными частотами становится больше и провал становится глубже.

Полоса пропускания связанных контуров

Ширина полосы пропускания зависит от двух факторов:

1. От коэффициента связи

2. От добротности контура.

Чтобы учесть оба этих параметра, вводят такое понятие, как фактор связи.

Зависимость фактора связи связанного контура от фактора связи одиночного контура.

РИСУНОК

При факторе связи 2,4 полоса пропускания связанных контуров примерно в три раза больше, чем у одиночных. Дальнейшее увеличение ширины полосы пропускания невозможно, поскольку провал в АЧХ опустится ниже уровня .

Главная особенность связанных контуров – лучшая прямоугольность АЧХ по сравнению с одиночными. Зависимость коэффициента прямоугольности от фактора связи следующая:

РИСУНОК

Коэффициент прямоугольности при факторе связи 2,4 не очень маленький, примерно 6.

Естественный способ дальнейшего улучшения избирательности – увеличение количества связанных контуров. Коэффициент прямоугольности будет улучшаться с увеличением числа контуров. При этом растут и потери. И максимальное количество связанных контуров не превышает 10. При этом 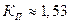. Дальнейшее снижение коэффициента прямоугольности могут обеспечить цифровые фильтры.

Передача и преобразование сигналов линейными цепями

Метод дифференциальных уравнений

Вопросы:

1. Общая характеристика методов анализа процессов в линейных цепях.

2. Метод дифференциальных уравнений

Задача анализа цепи сводится к следующему:

РИСУНОК

Известна линейная цепь, т.е. схема и все элементы. Известен входной сигнал . Задача – найти реакцию цепи 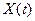- выходной сигнал. Ранее эта задача решалась для установившегося режима.

return false">ссылка скрыта

е

Для переходных процессов (процесс перехода от одного установившегося режима к другому), задача решается намного сложнее.

РИСУНОК

Задача – найти реакцию

Для решения данной задачи разработан ряд методов. Они все делятся на две группы:

1. Прямые методы – классический, операторный.

2. Суперпозиционные методы – временные, спектральные.

Сущность прямых методов сводится к составлению и решения дифференциального или операторного уравнения цепи. При этом, и входной сигнал , и реакция 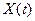рассматриваются как единое целое.

Суперпозиционные методы предполагают представление входного сигнала в виде суммы более простых сигналов

На каждое простое слагаемое 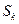отыскивается реакция

Полное описание процессов в цепи возможно при использовании мгновенных значений напряжений или токов, которые связаны друг с другом интегральными или дифференциальными зависимостями. Т.е. уравнения цепи, составленные на основании законов Ома и Кирхгофа будут дифференциальными уравнениями. Для цепи с неизменными параметрами, дифференциальные уравнения будут иметь постоянные коэффициенты, т.е. будут линейными дифференциальными уравнениями ЛДУ.

Дифференциальные уравнения цепи

В общем виде, дифференциальное уравнение любой цепи имеет следующий вид:

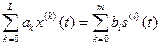
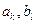- постоянные коэффициенты

- входной сигнал и реакция на него

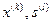- производные входного сигнала и реакции на него

Порядок уравнения, т.е. самое большое значение определяется самым большим порядком производной, а это в свою очередь зависит от сложности цепи. Пример:

Составит дифференциальное уравнение для цепи, где входной сигнал – ЭДС, выходной сигнал – ток, в момент времени .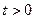

РИСУНОК

Согласно второму закону Кирхгофа,

Уравнение получилось интегро-дифференциальное. Дифференцируем уравнение по времени:

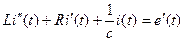
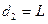
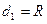
Данная цепи является цепью второго порядка.

Принужденные и свободные процессы.

Решение дифференциальных уравнений ищется в виде двух составляющих:

- общее решение

- частное решение

В радиотехнике эти решения называются свободной и принужденной составляющей.

Свободная составляющая описывает процессы в цепи, происходящие за счет собственных запасов энергии, т.е. при отключении источника.

Принужденная составляющая описывает процессы в цепи, происходящие под воздействием внешнего источника.

Свободная составляющая -

Для того, чтобы решить ЛОДУ надо сначала найти корни характеристического уравнения

.

Обозначим эти корни 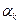. Количество этих корней зависит от степени уравнения. И тогда свободная составляющая

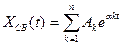- сумма экспонент.

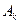- постоянные интегрирования. Они определяются исходя из начальных условий.

Решение 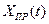получается как

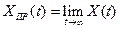
Чаще всего это находится из простых физических соображений.

РИСУНОК

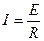
Начальные условия

Под начальными условиями понимают значения токов в индуктивностях и напряжений на емкостях цепи до начала переходного процесса. Если в момент коммутации ток на индуктивности и напряжение на емкости равно 0, то такие начальные условия называются нулевыми.

Ток и напряжение после коммутации, т.е. в момент времени зависят от того, какими они были непосредственно до коммутации.

Первый закон коммутации:

В ветви, содержащей индуктивность, скачок тока не возможен.

Второй закон коммутации:

Скачок напряжения на емкости невозможен

Расчет реакции цепи операторным методом

Составлено дифференциальное уравнение

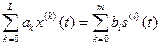
То его решение имеет вид

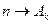
Дифференцируем правую и левую часть раз:

Решив эту систему получаем все коэффициенты , но решать ее нужно для момента времени .

Операторный (операционный) метод анализа линейных цепей

Вопросы:

1. Преобразования Лапласа

2. Законы Ома и Кирхгофа в операторной форме

3. Операторный способ решения дифференциальных уравнений. Учет начальных условий.

Метод дифференциальных уравнений является всеобщим и позволяет рассчитывать цепи любой сложности. Основной его недостаток – громоздкость. Решение уравнений третьего и более порядков вызывает определенные трудности. Чтобы избавится от этого применяют операторный метод. В основе операторного метода лежит переход от функции времени (оригиналов) к функциям комплексного переменного p – изображениям. Затем все действия выполнятся над изображениями, а в конце осуществляется обратный переход к оригиналу. Эту замену надо выполнить так, чтобы при этом исчезали производные. Это позволяет сделать преобразование Лапласа.

- прямое преобразование Лапласа

Если функция времени имеет ограниченный рост, то этот интеграл сходится и является функцией комплексной переменной

Реальные сигналы всегда ограничены, поэтому в радиотехнике преобразования Лапласа всегда применимы.

Обратный переход от изображений к оригиналам можно осуществить обратным преобразованием Лапласа.

- обратное преобразование Лапласа

Другой путь отыскания оригинала по изображению – таблицы операторных соответствий.

Как и у преобразования Фурье, у преобразования Лапласа есть ряд свойств:

- свойство линейности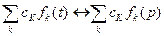

.

.

.

Обратное преобразование Лапласа, таблицы операторных соответствий, таблицы разложения.

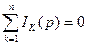- алгебраическая сумма изображений токов в узле рана 0 – первый закон Кирхгофа

- алгебраическая сумма изображений напряжений в контуре равна алгебраической сумме изображений ЭДС в контуре.

 

Вопросы:

1. Комплексная частотная характеристика

2. Переходная и импульсная характеристики

3. Связь между частотными и временными характеристиками

Задача остается прежней: на вход поступает сигнал на выходе . Суперпозиционные методы предполагают разбиение сигнала на ряд элементарных сигналов , затем отыскание реакции на каждый из этих сигналов и их суммирование. Одно из таких представлений – это представление сигнала в виде гармоник:

Или в комплексном виде

Для отыскания реакции используем комплексную частотную характеристику

 

Входной сигнал можно представить не только в виде суммы гармоник, но и в виде суммы единичных или дельта функций. Каждой из этих математических функций будет соответствовать своя реакция цепи.

Переходной характеристикой линейной цепи называется функция времени, равная реакции пустой линейной цепи на входное воздействие в виде единичной функции. Переходная характеристика – реакция на единичную функцию. Если входное воздействие представляет собой , то реакция будет в А раз больше. и - безразмерные величины, поэтому переходная характеристика в радиотехнике имеет размерность.

Физический смысл переходной характеристики заключается в том, что она показывает становление процессов в цепи при подключении к ней источника постоянного напряжения величиной 1В или источника постоянного тока величиной 1А.

Например, ели на колебательный контур подать напряжение в 1В, то напряжение на колебательном контуре будет идти следующим образом

РИСУНОК

Импульсная характеристика - это функция времени, отображающая реакцию пустой линейной цепи на входное воздействие в виде дельта импульса. Импульсная характеристика – это реакция цепи на дельта импульс на входе. Если на входе , на выходе получим А импульсных характеристик. Надо учитывать, что размерность дельта функций . Физически импульсная характеристика показывает, как будет выглядеть процесс на выходе цепи, если на вход подать дельта импульс.

Импульсная характеристика колебательного контура выглядит так

РИСУНОК

 

Таким образом известно четыре характеристики линейных цепей. . Все они выражают реакцию пустой цепи на какой-то стандартный сигнал. Эти стандартные сигналы линейно связанны между собой.

- преобразование Фурье от единицы

Линейная цепь не нарушает линейной связи, следовательно, и все характеристики цепи линейным образом связаны друг с другом.

Из этого соотношения следует, что если входной сигнал – дельта импульс , то

- изображение импульсной характеристики.

Поскольку изображение дельта импульса равно 1, то изображение импульсной характеристики равно передаточной функции

Известно, что изображение единичной функции равняется

Тогда изображение переходной характеристики можно получить из изображения импульсной

 

Таким образом, зная одну из характеристик цепи можно определить все остальные.

 

Элементарные линейные звенья и их характеристики

Вопросы:

1. Дифференцирующее звено.

2. Интегрирующее звено.

3. Колебательное звено.

Существует ряд типовых цепей, которые наиболее часто встречаются в радиотехнических цепях. К ним относятся дифференцирующее, интегрирующее и колебательное.

Реакция дифференцирующей цепи должна быть связана с входным сигналом

Идеальной дифференцирующей цепью была бы индуктивность или емкость

Однако использование таких элементов никогда не будет идеальным.

Реальные дифференцирующие цепи имеют такую схему:

РИСУНОК

Получим характеристики такой цепи:

- постоянная времени цепи

Если в h(t)подставить , то

Т.е. постоянная времени линейной цепи первого порядка – это время, за которое уровень напряжения (тока) уменьшается в e раз.

Все эти соотношения относятся и к цепи, только постоянная времени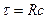

Т.е. условие, при котором фильтр верхних частот становится дифференцирующим звеном

 

Интегрирующая цепь – это такая цепь, реакция которого связана со входным сигналом соотношением

Идеальная интегрирующая цепь – это емкость или индуктивность

Реальное интегрирующее звено выглядит так:

РИСУНОК

Т.е. это фильтр нижних частот.

Характеристики:

Условие хорошего интегрирования

 

Колебательное звено относится к цепям второго порядка. Уравнение зависимости выходного сигнала от входного описывается дифференциальным уравнением второго порядка.

РИСУНОК

Если мы подадим на такую цепь единичную функцию, то рано или поздно колебания затухнут и установятся на уровне этой 1.

- коэффициент затухания

Импульсная характеристика такой цепи

РИСУНОК

Постоянная времени применима только для цепей первого порядка.

 

Спектральный метод или метод интеграла Фурье

Применение спектрального метода предполагает разложение входного сигнала на составляющие следующего вида:

И тогда выходной сигнал будет представлять собой слагаемые следующего вида:

При этом

Таким образом, основная задача в этом методе – представить входной сигнал в виде суммы гармоник. При этом возможны три ситуации:

- входной сигнал многотональный гармонический

Т.е. входной сигнал уже представляет собой сумму гармоник

-

В этом случае входной сигнал раскладывается в ряд Фурье:

- частота повторения

Коэффициент ряда Фурье

- спектральная плотность одиночного импульса

- входной сигнал – одиночный импульс, или любой другой непериодический сигнал.

Находим спектральную плотность входного сигнала

- прямое преобразование Фурье

Находим спектральную плотность выходного сигнала

Выходной сигнал

Достоинство спектрального метода – это наглядность в представлении прохождения сигналов через цепь.

Недостаток метода – основной класс функций, получающихся под знаком интеграла в обратном преобразовании Фурье и поддающихся аналитическому решению очень небольшой. Чаще всего получаются не берущиеся интегралы. В радиотехнике большее распространение получило дискретное преобразование Фурье.

 

Устойчивость линейных цепей

Основные понятия и определения устойчивости

В радиотехнике под понятием обратной связи понимают передачу сигнала с выхода на вход. Это применяется в автогенераторах, системах автоматического управления, системах слежения и многих других.

Характеристики систем с обратной связью значительно отличаются от характеристик систем без обратной связи.

Характеристики систем без обратной связи

Любую линейную цепь можно задать с помощью линейного дифференциального уравнения следующего вида:

Если перейти в область изображений, то

Любая активная линейная цепь состоит из элементов , можно утверждать следующее:

- корни полинома знаменателя передаточной функции (корни характеристического полинома или полюсы передаточной функции) не могут быть положительными.

Если корни характеристического полинома комплексные, то их вещественные части не могут быть положительными. Другими словами, все полюсы передаточной функции находятся в левой полуплоскости.

- временные характеристики не содержат экспонент вида с положительными .

Характеристики цепей с обратной связью

РИСУНОК

Получим передаточную функцию такой системы:

- передаточная функция цепи с обратной связью

Характеристики разомкнутой цепи очень важны для анализа цепей с обратной связью.

Рассмотрим следующие случаи:

1.

Система будет неустойчивой.

В этом случае, корни характеристического полинома

Могут иметь положительные действительные части. Это значит, что полюсы передаточной функции цепи с обратной связью могут лежать в правой полуплоскости на комплексной плоскости.

2.

Такая обратная связь называется положительной (ПОС).

Положительная обратная связь – это такая обратная связь, которая способствует удалению системы от состояния равновесия.

3.

Такая обратная связь называется отрицательной (ООС).

Отрицательная обратная связь – такая обратная связь, которая способствует возвращению системы в невозмущенное состояние.