Изоморфизм графов
Пусть  и
и 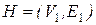 - графы и
- графы и 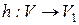 - взаимно-однозначное соответствие. (Заметим, что
- взаимно-однозначное соответствие. (Заметим, что 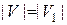 ). Отображение называется изоморфизмом графов
). Отображение называется изоморфизмом графов  и
и  , если для любых вершин
, если для любых вершин  и
и  графа
графа  их образы
их образы 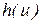 и
и 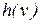 смежные в графе
смежные в графе  тогда и только тогда, когда
тогда и только тогда, когда  и
и  смежные в
смежные в  . Если такое отображение существует, то графы
. Если такое отображение существует, то графы  и
и  называются изоморфными.
называются изоморфными.
Очевидно, что отношение изоморфизма графов является отношением эквивалентности.
Другими словами: графы  и
и  изоморфны, если существует такое взаимно-однозначное соответствие между множеством вершин
изоморфны, если существует такое взаимно-однозначное соответствие между множеством вершин  и
и  , что любые две вершины одного графа смежные тогда и только тогда, когда соответствующие им вершины другого графа также смежны. На рис. 2.8. приведены изоморфные графы:
, что любые две вершины одного графа смежные тогда и только тогда, когда соответствующие им вершины другого графа также смежны. На рис. 2.8. приведены изоморфные графы:  и
и  ;
;  и
и  .
.
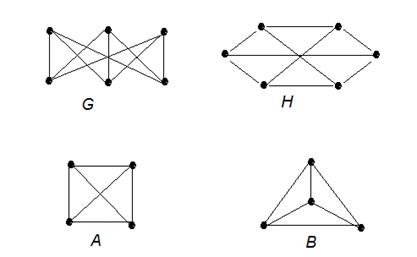
Рис. 2.8
Теорема. Графы изоморфны тогда и только тогда, когда их матрицы смежностей можно получить одну из другой одинаковыми перестановками строк и столбцов.
Доказательство.
Пусть заданы два изоморфных графа.  и
и  . Перенумеруем вершины графов
. Перенумеруем вершины графов  и
и  целыми числами от 0 до
целыми числами от 0 до  .
.  .
. 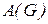 и
и 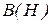 - матрицы смежностей графов
- матрицы смежностей графов  и
и  соответственно. Если
соответственно. Если 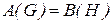 , то все доказано. В противном случае графы
, то все доказано. В противном случае графы  и
и  отличаются лишь нумерацией вершин. Значит, существует такая подстановка
отличаются лишь нумерацией вершин. Значит, существует такая подстановка 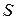 на множестве вершин
на множестве вершин  , которая сохраняет смежность, т.е. если
, которая сохраняет смежность, т.е. если 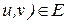 , то
, то 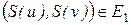 . Тогда получаем
. Тогда получаем 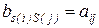 , где
, где 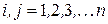 . Теорема доказана.
. Теорема доказана.
Следует заметить, что теорема об изоморфизме графов остается справедливой, если рассматривать не матрицы смежностей, а матрицы Кирхгофа.