РАЗДЕЛ XI: НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
11.1. Определение и свойства:
Определение:
Функция  называется первообразной функции
называется первообразной функции  в промежутке
в промежутке  , если в каждой точке этого промежутка выполняется равенства:
, если в каждой точке этого промежутка выполняется равенства:  или
или
 .
.
Определение:
Совокупность всех первообразных функции  в
в  называется неопределенным интегралом от этой функции в данном промежутке.
называется неопределенным интегралом от этой функции в данном промежутке.
Обозначение:  .
.
Основные свойства неопределенного интеграла:
1. 
2. 
3. 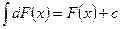
4. 
5. 
6. Если  то
то  , где
, где  - любая непрерывно - дифференцируемая функция.
- любая непрерывно - дифференцируемая функция.
1.2 Таблица дифференциалов и интегралов:
| Таблица интегралов | Таблица дифференциалов |
1. 
| 1. 
|
2. 
| 2. 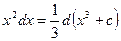
|
3. 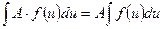
| 3. 
|
4. 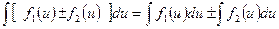
| 4. 
|
5. 
| 5. 
|
6. 
| 6. 
|
7. 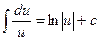
| 7. 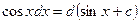
|
8. 
| 8. 
|
9. 
| 9. 
|
10. 
| 10. 
|
11. 
| 11. 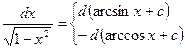
|
12. 
| 12. 
|
13. 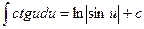
| 13. 
|
14. 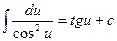
| 14. 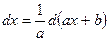
|
15. 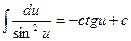
| 15. 
|
16. 
| |
17. 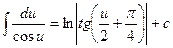
| |
18. 
| |
19. 
| |
20. 
| |
21. 
| |
22.  23.
23. 
|
11.3 Общие методы интегрирования:
1. Непосредственное интегрирование: подинтегральное выражение преобразуют так, чтобы заданный интеграл можно было представить в виде одного или алгебраической суммы нескольких табличных интегралов.
2. Способ подстановки: вводят новую переменную интегрирования, так чтобы интеграл с новой переменной или был бы табличным или брался бы одним из известных способов, т.е.  .
.
Алгоритм вычисления  :
:
1) Вводим новую переменную интегрирования  .
.
2) Представляем заданное подынтегральное выражение в переменных  и
и 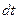 .
.
3) Берем интеграл с новой переменной.
4) В полученной первообразной заменяем переменную  на
на  .
.
Применяется в случае:
- если  , то
, то  ;
; 
-если 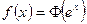 , то
, то  ;
;
- если  , то
, то  ;
;
- если  , то
, то  ;
;
- если  - действительные числа
- действительные числа  ,
, 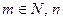 - любое
- любое  ,
,  , то
, то  .
.
3. Интегрирование по частям:
Применяется при интегрировании специально подобранных функций.
 - формула интегрирования по частям, где
- формула интегрирования по частям, где  - непрерывно - дифференцируемы при всех рассматриваемых
- непрерывно - дифференцируемы при всех рассматриваемых  .
.
Алгоритм нахождения  :
:
1) Разбиваем заданное подынтегральное выражение  на два множителя
на два множителя  и
и  .
.
2) Находим  и
и  .
.
3) К заданному интегралу применяем формулу 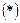 .
.
Классы функций, интегрируемых по частям:
1 класс:  ,
,
Здесь -  , где
, где  - многочлен любой степени, кроме нуля,
- многочлен любой степени, кроме нуля,  - любое ненулевое действительное число.
- любое ненулевое действительное число.
2 класс: 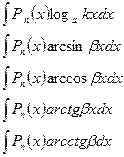 ,
,
Здесь -  , где
, где  - многочлен любой степени, включая нулевую,
- многочлен любой степени, включая нулевую,  - любое ненулевое действительное число.
- любое ненулевое действительное число.
3 класс:  , где
, где  - любое ненулевое действительное число.
- любое ненулевое действительное число.
Здесь выбор  безразличен.
безразличен.
Замечания:
1) при нахождении интегралов первого класса формулу интегрирования по частям применяют столько раз, какова степень данного многочлена  .
.
2) Нахождение интегралов третьего класса в итоге сводится к решению уравнения относительно заданного интеграла.
4. Интегрирование рациональных дробей:
Алгоритм нахождения  :
:
- Проверяем, является ли заданная рациональная дробь  правильной, если дробь неправильная, то представляем ее в виде суммы целой части и правильной рациональной дроби (для этого в общем случае делим числитель на знаменатель, в частности используем формулы сокращенного умножения)
правильной, если дробь неправильная, то представляем ее в виде суммы целой части и правильной рациональной дроби (для этого в общем случае делим числитель на знаменатель, в частности используем формулы сокращенного умножения)
- Раскладываем правильную рациональную дробь на сумму простейших методом неопределенных коэффициентов.
Определение: правильные рациональные дроби вида
 , где
, где  - любые действительные числа
- любые действительные числа 
 , где
, где  - любые действительные числа,
- любые действительные числа, 
 , где
, где 
 , где
, где 
называются простейшими дробями 1-4 типов.
Алгоритм представления правильной рац. дроби в виде суммы простейших дробей:
- каждому простому действительному корню 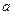 знаменателя соответствует одна дробь
знаменателя соответствует одна дробь  ;
;
- каждому  кратному действительному корню знаменателя соответствуют одна дробь
кратному действительному корню знаменателя соответствуют одна дробь 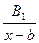 и
и 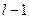 дробь:
дробь: 
- каждой простой паре комплексно-сопряженных корней знаменателя соответствует одна дробь  ;
;
- каждой  - кратной паре комплексно-сопряженных корней знаменателя соответствуют дробь
- кратной паре комплексно-сопряженных корней знаменателя соответствуют дробь  и
и 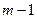 дробь:
дробь: 
Алгоритм нахождения коэффициентов разложения правильной рац. дроби:
- приводим правую часть разложения к общему знаменателю, получаем тождественное равенство двух дробей с одинаковыми знаменателями;
- отбрасываем эти знаменатели, получаем тождество из числителей;
- в последнем тождестве последовательно придаем значения действительных корней знаменателя исходной дроби, если они есть, а затем нужное число раз сравниваем коэффициенты при одинаковых степенях  . Получаем СЛАУ относительно искомых коэффициентов;
. Получаем СЛАУ относительно искомых коэффициентов;
- решив СЛАУ, находим коэффициенты и ,значит, само разложение;
- Интегрируем простейшие дроби и, если есть, целую часть:
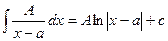



 - интегрируем либо по формуле Остроградского, либо с помощью реккурентных преобразований.
- интегрируем либо по формуле Остроградского, либо с помощью реккурентных преобразований.
5. Интегрирование функций, рационально зависящих от тригонометрических:
1. 
2. 
3. 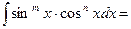

4.  ;
; 
5.  ;
;
 .
.
6. 

 .
.
6. Интегрирование простейших алгебраических иррациональностей:
1)  , где
, где 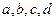 - любые действительные числа,
- любые действительные числа,  ,
,  - любые натуральные числа, составляющие несократимые дроби.
- любые натуральные числа, составляющие несократимые дроби.
Здесь 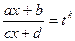 , где
, где  - общий знаменатель дробей
- общий знаменатель дробей  ;
;
2) 

 , где
, где 
3)  , где
, где  -любые действительны числа неравные нулю.
-любые действительны числа неравные нулю.
4)  - выделяем полный квадрат под знаком корня.
- выделяем полный квадрат под знаком корня.
5)  ;
;
6)  - в числителе получают дифференциал подкоренного выражения;
- в числителе получают дифференциал подкоренного выражения;
7)  , где
, где  - любые неравные нулю действительные числа,
- любые неравные нулю действительные числа,  - рациональные числа
- рациональные числа  :
:
- если  - целое, то полагают
- целое, то полагают  , где
, где  - общий знаменатель дробей
- общий знаменатель дробей 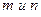 ;
;
- если  - целое, то
- целое, то  , где
, где  - знаменатель дроби
- знаменатель дроби  ;
;
- если 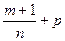 - целое, то
- целое, то  , где
, где  - знаменатель дроби
- знаменатель дроби  .
.
Неберущиеся интегралы:
 ;
; 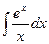 ;
;  ;
;  ;
;  ;
;  ;
;  ;
;
 .
.