Реализация проблемного подхода при изучении геометрического материала
Знакомство с геометрическими фигурами и телами происходит на первых же уроках, где эти фигуры используются в качестве объектов счета предметов. В дальнейшем, согласно программе того или иного года обучения, даются описания или простейшие определения геометрических понятий.
Каждое геометрическое понятие должно быть правильно воспринято и осмысленно усвоено на уроке всеми учащимися. Одним из эффективных средств для достижения этой цели является использование проблемного подхода, который заключается в создании перед учащимися проблемных ситуаций, их осознании, принятии и разрешении в процессе взаимодействия учителя и учащихся при максимальной самостоятельности последних. Выбор способа создания проблемной ситуациизависит в первую очередь от приема раскрытия содержания понятий, от уровня их изучения и от педагогического мастерства учителя.
Немалое значение имеют также познавательные, эмоционально-волевые, мотивационно - потребностные особенности учащихся. Особенно важно, чтобы предлагаемый материал находился в зоне ближайшего развития ученика, так как, по мнению крупнейшего специалиста по проблемным ситуациям в мышлении и обучении А.М. Матюшкина, «процесс мышления возникает лишь при определенной степени рассогласования между усвоенными и усваиваемыми знаниями, соответствующей некоторой единице, определяемой творческими возможностями и уровнем развития субъекта. Собственно, только в этом относительно узком диапазоне рассогласования и возможен процесс мышления, приводящий к выявлению неизвестного в возникающей проблемной ситуации» [3].
Опираясь на эти требования, учитель при планировании урока должен разумно сочетать наглядность, проблемные вопросы и задания, проблемный диалог, чтобы каждый ученик включился в самостоятельную поисковую деятельность по решению проблем и «открытию понятий».
Использование проблемного диалогана уроках математики, как и другие формы обучения, требует от его участников определенного опыта. Для введения учащихся в ситуацию диалога рекомендуем учителям использовать такие элементы как:
– диагностика готовности учащихся к диалогическому общению;
– наличие базовых знаний;
– установка на самоизложение и восприятие иных точек зрения;
– поиск опорных мотивов, т.е. тех волнующих учащихся начальных классов вопросов и проблем, благодаря которым может сложиться собственное осмысление изучаемого материала;
– переработка учебного материала в систему проблемно - конфликтных вопросов и заданий (задач);
– проработка различных возможных вариантов развития сюжетных линий диалога;
– проектирование способов взаимодействия младших школьников, их участия в дискуссии, их возможных ролей;
– гипотетическое выявление зон импровизации, т.е. таких суждений в диалоге, которые трудно заранее предусмотреть.
Особое значение для диалогического общения имеет умение учителя задавать вопросы.
Как мы знаем, вопросы могут формулироваться по_разному. Сравним несколько вариантов постановки вопроса, которые требуют от ученика начальных классов знаний понятия «равнобедренный треугольник»:
2) Какой треугольник называется равнобедренным?
3) Какие условия необходимы, чтобы треугольник был равнобедренным?
4) На каком основании можно сделать вывод, что треугольник является равнобедренным?
Первые два варианта мы называем репродуктивными вопросами, так как ответы на них предполагают только воспроизведение определения равно бедренного треугольника, а третий и четвертый вопросы, названные нами проблемными, стимулируют ребенка к размышлению, анализу, выбору вариантов ответа, доказательству, а также дают возможность другим ученикам участвовать в дискуссии.
Выделим некоторые требования, которые помогут учителям в овладении умением задавать ученикам корректные вопросы.
1. Вопросы должны быть поставлены ясно и четко.
2. Поиск ответа должен вызвать у ученика определенное умственное усилие и желание высказать собственное мнение.
3. Вопросы того или иного этапа урока должны быть выстроены в строгой последовательности и соответствовать определенной системе.
4. Ценность вопроса возрастает, ког-
Рис. 1

да он сопровождается эмоциональной окраской или наглядным материалом.
Поясним сказанное на примере ознакомления учеников начальных классов с понятиями «круг» и «окружность», когда учитель задает классу репродуктивные и проблемные вопросы, выстроенные в строгой логической последовательности.
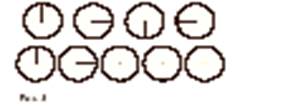
На доске нарисованы различные фигуры (см. рис. 1).
Вопросы и задания ученикам:
1) Какие из нарисованных на доске фигур можно назвать линиями? (Все.)
2) Уточните, какие из нарисованных на доске линий являются ломаными, а какие – кривыми? (2, 4 – ломаные линии; 1, 3, 5, 6, 7, 8, 9 – кривые.)
3) Разделите кривые линии на две группы: замкнутые и незамкнутые. Какие фигуры окажутся в первой группе, а какие – во второй? (Замкнтые кривые линии – 3, 6, 7, 8; незамкнутые – 1, 5, 9.)
4) В фигурах 3, 6, 8, которые являются замкнутыми кривыми линиями, расставлены точки. Можно ли утверждать, что расстояния от точки О до точек А, В, С, D в каждой фигуре одинаковые? (В фигуре 6 расстояния от точки О до точек А, В, С, D не одинаковые, а в фигурах 3 и 8 – одинаковые.)
5) К доске приглашаются три ученика, которым предстоит убедить класс в том, что расстояния от точки О до точек А, В, С, D в фигурах 3 и 8 одинаковые, а в фигуре 6 – разные, измерив эти расстояния при помощи линейки или циркуля.
6) Остальные ученики класса сравнивают фигуры 6 и 8. (Сходство: замкнутые кривые линии имеют внутри точку, отмеченную буквой О, на самих замкнутых кривых линиях отмечены точки А, В, С, D. Отличия: расстояния от точки О до точек А, В, С, D в фигуре 6 – разные, в фигуре 8– одинаковые.)
7) Как вы думаете, почему фигура 8 является окружностью, а фигура 6 не является окружностью? (Потому что в фигуре 8 расстояния от точки О до точек А, В, С, D, а также а в фигуре 6 – разные.)
8) Назовите существенные признаки окружности. (Это кривая замкнутая линия; расстояния от точки О, называемой центром, до всех точек на окружности одинаковые.)
9) Можно ли назвать окружностями фигуры 5, 7, 9? (Нет. Фигуры 9 и 5 не являются замкнутыми кривыми, а фигура 7 не имеет центра, расстояния от которого до всех точек фигуры были бы одинаковыми.)
10) Чем отличаются окружности 3 и 8? (Расстоянием от точки О до точек на окружности.)
11) Если мы отметим любую другую точку на окружности 8 и измерим расстояние от точки О – центра окружности – до данной точки, оно будет одинаковым с расстоянием от точки О до точек А, В, С, D? (Да.)
12) Расстояние от центра окружности О до любой точки на окружности называется радиусом и обычно обозначается латинской буквой R.
Используя циркуль, постройте в тетрадях две окружности с одинаковым радиусом, равным 2 см.
13) Закрасьте ту часть тетрадного листа, которая ограничена первой окружностью. (Пока ученики выполняют это задание, учитель вывешивает на доске большой лист бумаги с таким же рисунком, как у учеников.)
return false">ссылка скрыта14) Как вы думаете, чем можно объяснить, что первая фигура называется кругом, а не окружностью? (Первая фигура закрашена, т.е. ей принадлежат все точки, находящиеся внутри этой фигуры, и она называется кругом.)
16) Чем отличается круг от окружности?
17) Послушайте стихотворение и постарайтесь разрешить спор, возникший между кругом и окружностью:
Рис. 2

Встретились окружность с кругом,
Спорить стали вот о чем:
Кто главнее всех в округе?
Кто сначала, кто потом?
Круг сказал, что он главнее:
«Я большой и, посмотри,
Весь заполнен в середине,
И по краю, и внутри».
Тут воскликнула окружность:
«Жить не сможешь без меня!
Я не просто загогулька –
А граница я твоя!»
Долго спорили фигуры,
Кто из них кого главней,
И соседей опросили,
И знакомых, и друзей.
Но закончить этот спор
Не смогли и до сих пор,
В чью же пользу и без ссор
Разрешится этот спор?
(Ученики высказывают свои мнения о том, какую фигуру они считают «главнее».)
17) Какие знакомые вам предметы имеют форму круга, а какие – форму окружности?
На этапе знакомства с новыми геометрическими понятиями можно использовать в основном проблемные вопросы и задания. Их выполнение должно осуществляться в ходе совместной деятельности учителя и учащихся, в процессе анализа и сопоставления различных суждений, точек зрения, выделяющих существенные признаки изучаемых геометрических фигур.
Очень важное значение при изучении элементов геометрии надо отводить также заданиям, направленным на воспроизведение знаний и их применение. На этом этапе по мере возможности следует заменить репродуктивные задания на творческие, эвристические. Именно такие проблемные задания творческого характера помогают ученикам осмыслить учебный материал, ые задания на творческие, эвристические. Именно такие проблемные задания творческого характера помогают ученикам осмыслить учебный материал, закрепить полученные знания, научиться применять их в новой ситуации. Приведем несколько таких заданий, которые можно предложить ученикам на том же уроке по теме «Круг и окружность»:
1.Не нарушая закономерностей, нарисуй радиусы в последних окружности