Задания на построение

Задания на построение составляют важную часть системы формирования геометрических знаний и умений ребенка в начальной школе. Эти задания создают базу для развития пространственного воображения у ребенка, умения наблюдать, сравнивать, обобщать, анализировать и абстрагировать. Необходимость формирования

 

у ребенка практических умений построения геометрических фигур с помощью циркуля, угольника и линейки и подготовки к обучению рассуждениям и доказательству является важнейшей задачей курса начальной математики с точки зрения дальнейшего математического образования ребенка. Как доказано психологами, возраст ученика начальной школы является наиболее благоприятным в жизни человека возрастом для развития образного (а значит, и пространственного) мышления, формирования приемов умственных действий (сравнения, обобщения, абстрагирования и др.). Анализ особенностей этапов развития математического мышления ребенка показывает также необходимость организации подготовки к обучению доказательствам в период обучения в на­чальной школе.

Рассмотрим виды заданий на построение по годам обучения и покажем возможности их использования для развития указанных компонентов мышления.

1 класс

1. Начерти в тетради ломаную, состоящую из четырех звеньев. Сколько вершин у этой ломаной?

Выполнение:

По определению, концы каждого звена — это вершины ломаной. Таким образом, ломаная из 4 звеньев будет иметь 5 вершин.

2. Вырежи из приложения нужные фигуры и составь из них домик, кораблик, рыбку (по рисунку, данному в учебнике).

Выполнение:

Задания такого вида представляют собой конструктивные задачи на развитие операции синтеза (конструирование целого из частей). В учебнике эти задания встречаются вплоть до 4 класса, но особенно важны они в 1 классе. Если у ребенка возникают затруднения, следует сделать для него увеличенный вариант рисунка, чтобы можно было складывать заданную фигуру, накладывая ее части прямо на рисунок.

Эти задания являются подготовительными для заданий вида: сколько на чертеже треугольников, четырехугольников и т. п.

В их основе лежит операция анализа (умение мысленно «разобрать» объект на составные части и выделить каждую из них). Практика показывает, что при хорошей подготовке посредством выполнения заданий на конструирование (синтез), задания дан­ного вида даются ребенку намного легче.

3. Начерти один четырехугольник. Проведи 1 отрезок, что­бы получилось 2 треугольника.

Выполнение:

При выполнении данного задания полезно рассмотреть разные варианты его выполнения — это развивает гибкость мышления и пространственное воображение. Полезно сравнить полученные результаты, сделав обобщение: для того чтобы получилось 2 тре­угольника, нужно проводить в четырехугольнике диагональ.

4. Как можно провести в треугольнике 1 отрезок так, чтобы получилось 3 треугольника? Выполнение:

Достаточно провести 1 отрезок так, чтобы разделить данный треугольник на 2 треугольника. В качестве третьего рассматриваем исходный треугольник (содержащий два меньших).

5. Составь из 7 палочек 2 одинаковых квадрата, а из 10 палочек 1 большой квадрат и 1 маленький.

Выполнение:

Задание на конструирование из палочек (см. характеристику задания 2).

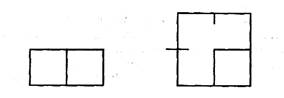
6. Начерти одну ломаную, у которой 4 звена и 5 вершин, а другую — у которой 4 звена и 4 вершины.

Выполнение:

См. характеристику задания 1.

7. Начерти любой четырехугольник и проведи в нем 2 отрезка так, чтобы получилось 8 треугольников.

Выполнение:

При выполнении данного задания полезно рассмотреть разные варианты его выполнения — это развивает гибкость мышления и пространственное воображение. Полезно сравнить полученные результаты, сделав обобщение: для того, чтобы получилось 8 треугольников, нужно проводить в четырехугольнике две диагонали.

Каждый четырехугольник содержит 4 маленьких треугольника, а также 4 треугольника, составленных из двух расположенных рядом маленьких треугольников.

2 класс

1. Проведи прямую, отметь на ней 3 точки. Сколько всего отрезков получилось?

Выполнение: ---------•----------•------------------•—

Задание аналитического характера: всего отрезков три: два меньших, обозначенных точками, и в качестве третьего рассматриваем отрезок, содержащий оба меньших отрезка (фактически: два отрезка являются частями третьего).

2. Начерти и дополни до прямоугольника:

Выполнение:

Задание развивает воссоздающее воображение, требует воссоздания целого по его частям. Поскольку в учебнике эти задания даны на клетчатой основе, их выполнение не требует применения инструментов при построении, достаточно производить ориентировку на количество клеточек, восстанавливая форму заданной фигуры.

3. Как провести в каждом из этих четырехугольников 1 отрезок, чтобы получился квадрат?

Выполнение:

Задание обратное по типу заданию 2. Требует анализа и выде­ления части из целого. Оно также дано в учебнике на клетчатой основе, поэтому не требует применения инструментов. Для его выполнения достаточно ориентировки по клеточкам и соблюдения равенства сторон квадрата.

4. Сложи из треугольников нарисованные фигуры (по рисунку в учебнике).

Выполнение:

См. выше характеристику задания 2 из 1 класса.

3 класс

1. Начерти два отрезка так, чтобы длина одного была в два раза больше длины данного отрезка, а длина другого — в 2 раза меньше длины данного.

Выполнение:

Чтобы начертить отрезок в 2 раза больше данного, можно измерить его циркулем, и отложить на прямой последовательно два таких отрезка:

Полученный таким образом отрезок будет в два раза больше дан­ного.

Чтобы начертить отрезок в два раза меньше данного, нужно разделить данный отрезок пополам, и построить отрезок, равный половине данного. Поскольку техника деления отрезка пополам с помощью циркуля предлагается детям для знакомства только на последней странице учебника 4 класса, очевидно, предполагается, что для выполнения этого задания следует использовать измерение и вычисление длины искомого отрезка, а потом его построе­ние по известной длине.

Можно познакомить ребенка с техникой деления отрезка пополам с помощью циркуля:

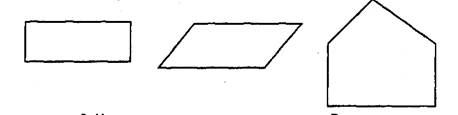
2. Начерти на клетчатой бумаге и вырежи прямоугольник и два треугольника, как на чертеже.

Составь из этих фигур: четырехугольник, пятиугольник. Сравни площади составленных фигур.

Выполнение:

Задание конструктивного характера. Цель задания — показать ребенку, что равносоставленные фигуры имеют равные площади. Полезно составить различные по форме четырехугольники и убедиться в том, что пятиугольник получается только одной формы:

3. Начерти три таких четырехугольника. В каждом из них проведи один отрезок так, чтобы он разделил четырехугольник:

1) на два треугольника;

2) на треугольник и прямоугольник;

3) на квадрат и четырехугольник.

Выполнение:

См. характеристику задания 3 из 2 класса.

4. Начерти в тетради пятиугольник и покажи на чертеже, как можно двумя взмахами ножниц разрезать этот пятиугольник так, чтобы получилось 2 четырехугольника и 1 треугольник.

Выполнение:

Полезно рассмотреть разные варианты выполнения задания:

5. Начерти в тетради любую фигуру, кроме прямоугольника, так, чтобы ее площадь была 12 см2.

Выполнение:

По условию фигура не может быть прямоугольником (а значит, и квадратом). Площади фигур другой формы ученики 3 класса умеют находить только способом подсчета квадратных сантиметров. Значит, следует рисовать фигуру произвольной формы, состав­ленную из квадратиков по 1 см².

Другой, более сложный вариант: начертить прямоугольник площадью 24 см2. Разделить его пополам — получится треугольник площадью 12 с см².

4 класс

1. Начерти в тетради прямой, острый и тупой углы с общей вершиной в точке В разными цветными карандашами. Выполнение:

Полезно обратить внимание ребенка на то, что получается 2 тупых угла:

2. Начерти в тетради четырехугольник АВСО, как на рисунке. Проведи в нем отрезок ВМ так, чтобы угол ВМС был прямым.

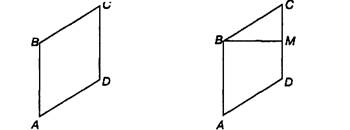
Выполнение:

Для выполнения задания фактически требуется умение опускать перпендикуляр из точки на прямую, однако здесь предполагается, что ребенок, используя угольник, ищет позицию совмещения его сторон с отрезком СО и точкой В.

3. Начерти отрезки, как показано на чертеже. Соедини точки так, чтобы получился четырехугольник. Проверь, квадрат ли это.

Выполнение:

Рисунок в учебнике дан на клетчатой основе, поэтому его копирование требует только подсчета клеток. Получившаяся фигура будет квадратом. Задание иллюстрирует свойство диагоналей квадрата: диагонали квадрата при пересечении образуют прямой угол и делятся в точке пересечения пополам.

4. Рассмотри чертеж и начерти в тетради квадрат, диагональ которого равна 4 см. Проведи окружность так, чтобы она прошла через все вершины квадрата.

Выполнение:

Задание, аналогичное заданию 3 с добавлением заданной длины диагонали. Выполняется на основе подсчета клеток и свойств диагоналей квадрата. Точка пересечения диагоналей квадрата является центром описанной (и вписанной) окружности.

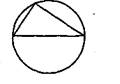
5. Начерти окружность, проведи в ней диаметр и соедини концы диаметра с любой точкой окружности. Какого вида тре­угольник получился?

Выполнение:

Получится прямоугольный треугольник. Задание иллюстрирует свойство вписанного угла, опирающегося на диаметр.

6. Начерти прямой угол с вершиной в точке О. Отложи от точки О на сторонах угла равные отрезки ОА и ОВ длиной по 3 см. Соедини отрезком точки Аи В., Какого вида треугольник получился? Дай два ответа.

Выполнение:

Получится равнобедренный треугольник, который также является прямоугольным.

 

7. Начерти разносторонний прямоугольный треугольник; равнобедренный тупоугольный треугольник.

Выполнение:

Задание проверяет умение ребенка соблюдать два заданных признака при выполнении чертежа:

Следует обратить внимание на то, что построение равнобедренного тупоугольного треугольника требует также знания способа построения равнобедренных треугольников.

8. Начерти любой прямоугольник, проведи в нем диагонали. Построй окружность с центром в точке их пересечения, которая проходит через все его вершины. (На полях дан полный чертеж.)

Выполнение:

Поскольку в учебнике дан на полях полный чертеж задания, оно требует лишь копирования образца.

Задание иллюстрирует следующее свойство прямоугольника: точка пересечения диагоналей прямоугольника является центром описанной окружности.

9. Начерти в тетради прямоугольник АВСО со сторонами 3 см и 4 см. Проведи в нем 2 отрезка так, чтобы получилось 8 треугольников.

Выполнение: См. характеристику задания 7 из 1 класса.

10. Построить равносторонний треугольник.

Выполнение:

В учебнике приведен полный чертеж, требуется лишь копирование образца.

11. Построить равнобедренный треугольник.

Выполнение:

См. характеристику задания 10.

12. Построить треугольник по трем заданным сторонам.

Выполнение:

См. характеристику задания 10.

13. Раздели отрезок пополам с помощью циркуля.

Выполнение:

См. характеристику задания 10.

Сравнение количества и качества заданий на построение и заданий на измерение и вычисление показывает, что заданиям на измерение и вычисление уделено в учебниках намного больше внимания. С качественной (а также перспективной) точки зрения, в дальнейшем ребенку будут необходимы в большей мере умения по построению и доказательству правильности построения, поскольку они лежат в основе умения решать задачи и доказывать теоремы в курсе геометрии и выполнять чертежи в курсе черчения.

 

Приложение 2.