Системы координат

 

8.1. Общегеографическая система координат

 

Принцип построения данной системы координат рассмотрен выше, в разделе 6.2. Данная система относится к плановым системам координат и позволяет определить долготу и широту любой точки, находящейся как на физической поверхности Земли (и в ее недрах), так и любой точки, находящейся на поверхности общего земного эллипсоида, либо референц-эллипсоида. При использовании общего земного эллипсоида, либо принятого референц-эллипсоида, координаты всех точек поверхности Земли могут быть определены в единой общегеографической системе (долгота и широта), т.е. она является абсолютной. Долготы и широты точек в географической системе координат определяют из астрономических наблюдений светил (звезд, Солнца).

 

 

8.2. Зональная система прямоугольных координат Гаусса

 

Поскольку каждая из проекций Гаусса-Крюгера передает на плоскость только фрагмент поверхности Земли, ограниченный меридианами через 6° долготы, то всего на поверхность Земли должно быть составлено 60 проекций (60 зон). Счет зон ведется от Гринвичского меридиана на восток: 1, 2, 3, … и т. д. Каждая зона совпадает по своему положению с границами колонны, номер которой определяет номенклатуру карты с учетом пояса, имеющего буквенное обозначение (см. раздел 10.1 Разграфка и номенклатура топографических карт). Чтобы получить номер зоны, необходимо из номера колонны вычесть 30, если номер колонны больше 30, и прибавить 30, если номер колонны меньше 30. В каждой из 60 проекций образуется отдельная система прямоугольных координат.

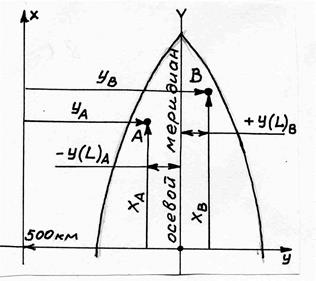Рис. 19. Зональная система прямоугольных координат Гаусса

 

Осью Х зональной системы координат Гаусса является осевой меридиан зоны, отнесенный на запад на 500 км (рис. 19). Осью У является проекция экватора, перпендикулярная оси Х. В самой зоне точка может находиться на восток или запад от осевого меридиана на расстоянии L. Для восточной части зоны значения L положительные, для западной – отрицательные. Связь между координатой У и значением L следующая:

У = 500 км + L (3)

Для указания принадлежности точки определенной зоне впереди координаты У приписывают номер соответствующей зоны.

Например, точка А расположена на расстоянии 5257 км от экватора и на расстоянии L = 82 км к западу от осевого меридиана 15-й зоны. В этом случае координаты точки А будут следующие: Х_А = 5257 км, У_А = 15418 км (418 = 500 – 82; запись читается так: 418 км в 15-й зоне). Для определения номера зоны по координате У необходимо влево отложить три позиции полных километров. Оставшееся впереди значение укажет номер зоны. Например, У = 16627, 544 км – 16-я зона 627,544 км; У = 5381625 м – 5-я зона 381625 м (381,625 км). Первая цифра в координате У после номера зоны не может быть нулем и девяткой.

 

8.2.1. Вычисление плоских прямоугольных координат Гаусса по географическим координатам

 

Плоские прямоугольные координаты Гаусса Х и У весьма сложно связаны с географическими координатами λ и φ точек земной поверхности.

Предположим, что некоторая точка А имеет географические координаты λ и φ. Поскольку разность долгот граничных меридианов зоны равна 6°, то соответственно для каждой из зон можно получить долготы крайних меридианов: 1-я зона (0° – 6°), 2-я зона (6° – 12°), 3-я зона (12° – 18°) и т.д. Таким образом, по географической долготе точки А можно определить номер зоны, в которой эта точка находится. При этом долгота λ _оn осевого меридиана зоны определится по формуле λ _оn = (6°n – 3°), в которой n – номер зоны.

Для определения плоских прямоугольных координат Х и У по географическим координатам λ и φ воспользуемся формулами, выведенными для территории России для референц-эллипсоида Красовского (референц-эллипсоид – фигура, максимально приближенная к фигуре Земли в той ее части, на которой находится данное государство, либо группа государств):

(4)

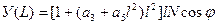(5)

В формулах (4) и (5) приняты следующие обозначения:

У(L) – расстояние от точки до осевого меридиана зоны;

l = (λ - λ_o)²/r² (разность долгот определяемой точки и осевого меридиана зоны в радианной мере; r² = 206264,8062² - число секунд в одном радиане);

φ _рад = φ ² / r² (широта точки, выраженная в радианной мере);

N = 6399698,902 - [21562,267 – (108,973 – 0,612 cos² φ) cos² φ ] cos² φ;

а_о = 32140,404 - [135,3302 – (0,7092 – 0,0040 cos² φ) cos² φ ] cos² φ;

а₃ = (0,3333333 + 0,001123 cos² φ) cos² φ – 0,1666667;

а₄ = (0,25 + 0,00252 cos² φ ) cos² φ – 0,04166;

а₅ = 0,0083 - [0,1667 - (0,1968 + 0,0040 cos² φ) cos² φ ] cos² φ;

а₆ = (0,166 cos² φ – 0,084) cos² φ.

Значения широт и долгот по указанным формулам вычисляют до 0,0001², а значения координат Х и У - до 0,001 м.

По формуле (5) значение координаты У(L) получают относительно осевого меридиана зоны, т.е. оно может получиться со знаками «плюс» для восточной части зоны или «минус» – для западной части зоны. Для записи координаты У в зональной системе координат необходимо вычислить расстояние до точки от осевого меридиана зоны, отнесенного на запад на 500 км, а впереди полученного значения приписать номер зоны. Например, получено значение У(L) = - 303678,774 м в 47 зоне. Тогда

У = 47 (500000,000 – 303678,774) = 47196321,226 м.

Пример вычисления плоских прямоугольных координат по геодезическим координатам приведен в разделе 8.2.2.

 

8.2.2. Вычисление географических координат по плоским прямоугольным координатам Гаусса

 

Для решения данной задачи также используются формулы пересчета, полученные для референц-эллипсоида Красовского.

Предположим, что нам необходимо вычислить географические координаты φ и λ точки А по ее плоским прямоугольным координатам Х и У, заданным в зональной системе координат. При этом значение координаты У записано с указанием номера зоны и с учетом переноса осевого меридиана зоны на запад на 500 км.

Предварительно по значению У находят номер зоны, в которой расположена определяемая точка, по номеру зоны определяют долготу λ _o осевого меридиана и по расстоянию от точки до отнесенного на запад осевого меридиана находят расстояние У(L) от точки до осевого меридиана зоны (последнее может быть со знаком плюс или минус).

Значения географических координат φ и λ по плоским прямоугольным координатам х и у находят по формулам:

φ = φ _х - [1 - ( b₄ – 0,12 z²) z² ] z² b₂ r² (6)

λ = λ _o + l (7)

l = [ 1 – ( b₃ - b₅ z²) z²] z r² (8)

В формулах (6) и (8) :

φ _x²= b² +{50221746 + [293622 + (2350 + 22cos²b)cos²b]cos²b}10^-10sinbcosb r²;

b² = ( Х / 6367558,4969) r²;

z = У(L) / ( N_x сos φ _x );

N_x = 6399698,902 - [21562,267 – (108,973 – 0,612 cos² φ _x) cos² φ _x] cos² φ _x;

b₂ = (0,5 + 0,003369 cos² φ _x ) sin φ _x cos φ _x ;

return false">ссылка скрыта

b₃ = 0,333333 – ( 0,166667 – 0,001123 cos² φ _x ) cos² φ _x ;

b₄ = 0,25 + (0,16161 + 0,00562 сos² φ _x) cos² φ _x ;

b₅ = 0,2 – (0,1667 – 0,0088 сos² φ _x) cos² φ _x .

Пример вычисления плоских прямоугольных координат Гаусса по географическим координатам и географических координат по плоским прямоугольным координатам Гаусса приведен в таблице 1. При определении координат обязательно выполняется расчет по обратному определению географических координат с целью подтверждения правильности выполненных расчетов. Т.е., если определяются прямоугольные координаты по географическим, то, используя полученные значения прямоугольных координат, необходимо вычислить географические координаты. Они должны совпасть с первоначальными. И наоборот, при вычислении географических координат по прямоугольным следует обратным расчетом проверить значения прямоугольных координат.

Пример

Вычислить прямоугольные координаты точки (с обратным контрольным расчетом), имеющей географические координаты λ = 65^о01'38,2456" и φ = 47^о02'15,0543" и находящейся в 11-й зоне (табл. 1).

 

Таблица 1

Вычисление плоских прямоугольных координат Х и У по географическим координатам φ и λ (с обратным перерасчетом)

 

№№ п/п	Параметр	Вычисление Х и У по φ и λ (значение параметра)	Параметр	Вычисление φ и λ по Х и У (значение параметра)
	φ°	47о02'15,0543"	βРАД	0,818760380
	φ"	169335,0543"	β"	168881,4511"
	φ"/ρ"	0,820959510	β°	46о54'41,4512"
	Sin φ	0,731800091	Sin β	0,730299573
	Cos φ	0,681519352	Cos β	0,683127026
	Cos2 φ	0,464468627	Cos2 β	0,466662533
	lo	+2о01'38,2456"	φ х РАД	0,821272741
	l"/ ρ"	+0,035382893	φ х"	169399,6627"
	N	6389707,353 м	φ х°	47о03'19,6628"
	ао	32077,69996	Sin φ х	0,732013528
	а4	0,075000799	Cos φ х	0,681290096
	а6	-0,003204001	Cos2 φ х	0,464156195
	а3	-0,011601574	Nx	6389714,058 м
	а5	-0,026270237	Nx Cos φ х	4353248,903 м
	l2	0,001251949	z	+0,035394247
	N l2	7999,587730 м	z2	0,001252753
	Х	5213504,617 м	φ	47о02'15,0541"
	У(L)	+154079,966 м	lо	+2о01'38,2456"
	У	11654079,966 м	λ	65о01'38,2456"

 

Примечания:

1. Во второй части таблицы не приведены значения коэффициентов b.

2.Расхождения в значениях φ, равное 0,0002" можно считать допустимым, поскольку ошибка в определении координаты Х в этом случае составляет примерно 7 мм (1" дуги примерно соответствует 33 м).

 

8.3. Система высот

 

Высота точки является третьей координатой точки на поверхности Земли и в ее недрах. Рассмотренные ранее системы координат (географических и прямоугольных) относятся к плановым системам, которые не определяют полностью положение точки на физической поверхности Земли.

В России принята Балтийская система высот. За нулевую высоту принят средний уровень Балтийского моря. Условно уровень моря продолжен под материками, и для определения высоты точки на суше или на морском дне необходимо определить расстояние по отвесной линии в данной точке до уровня Балтийского моря. Эти расстояния называют абсолютными высотами (рис. 20). Абсолютная высота Н считается положительной, если точка находится дальше от центра Земли, чем уровень Балтийского моря, и отрицательной, если точка находится по отношению к уровню моря со стороны центра Земли.

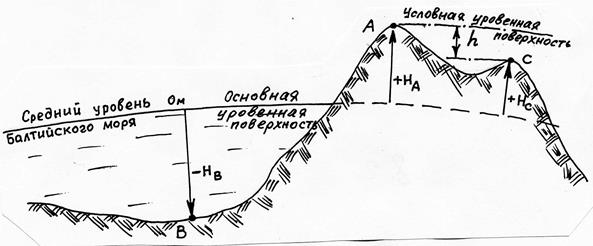
Рис. 20. Система высот. Абсолютные и относительные высоты

 

Часто определяют высоты точек не в абсолютной, а относительной форме, по отношению к какой-либо другой точке с известной или неизвестной высотой. Такие высоты называют относительными высотами или превышениями. Превышения обозначают буквой h.

Превышение – это разность абсолютных (или условных) высот двух точек: h_С = Н_С – Н_А. Оно может быть положительным или отрицательным (а также и равным нулю). Так, в соответствии с рис. 20, превышение точки С над точкой А – отрицательное, а превышение точки А над точкой С – положительное.

Условная высота может быть назначена для какой-либо точки на поверхности Земли, и высоты всех других точек в этом случае определяются относительно нее. Для перевода в Балтийскую систему высот необходимо определить высоту исходной точки в этой системе и перевычислить высоты всех других точек введением соответствующей одинаковой поправки.

 

8.4. Системы полярных координат

 

Для полярной системы координат характерно наличие полюса Р₁, полярной оси Р₁ Р₂, полярного угла β между направлением полярной оси и направлением на определяемую точку, расстояния d (горизонтального проложения – проекции линии местности на горизонтальную плоскость) – рис. 21 а.

Полярные углы обычно отсчитывают от полярной оси по направлению движения часовой стрелки.

В биполярной системе координат (рис. 21 б) имеется два полюса (Р₁ и Р₂), а положение точки однозначно определяется значениями двух горизонтальных углов β₁ и β₂, измеренных в точках полюсов (угловая засечка), либо значениями двух измеренных горизонтальных проложений d₁ и d₂ (линейная засечка). В том и другом случаях положение полюсов известно, т.е. известно и расстояние между ними.

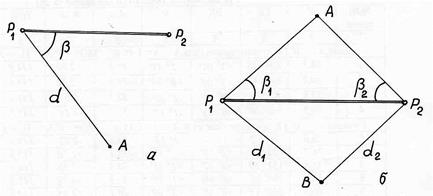
Рис. 21. Полярные системы координат

 

Указанные системы координат часто используют для получения координат точек местности при производстве топографической съемки. Засечка точек производится с известных на местности базисов, для концов которых отдельно определяют координаты, а также определяют дирекционный угол направления базиса.