Системы счисления и действия в них
Общая характеристика процессов сбора, передачи, обработки и накопления информации базируется на использовании кодирования информации средствами ее представления в виде чисел определенных систем счисления, в частности, двоичной, шестнадцатиричной.
Алфавит Х из р символов и правила записи (изображения) и обработки чисел с помощью символов этого алфавита называются системой счисления (нумерацией) с основанием р. Число х в системе с основанием р обозначается как (х)р или хр [1].
Любая система счисления– это система кодирования числовых величин (количеств), позволяющая выполнять операции кодирования и декодирования, то есть по любой количественной величине однозначно находить его кодовое представление и по любой кодовой записи – восстанавливать соответствующую ей числовую величину.
Все системы счисления строятся по общему принципу: определяется величина р – основание системы, а любое число х записывается в виде комбинации степеней веса р от 0-й до n-й степени следующим образом:
(x)10 = xnpn + xn–1pn–1 + ... + x1p1 + x0p0.
Наиболее используемые в информатике системы счисления кроме десятичной – это:
1) двоичная, над алфавитом Х = {0,1};
2) восьмеричная, над Х = {0, 1, 2, 3, 4, 5, 6, 7};
3) шестнадцатеричная, над Х = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F}, где символы А, В, С, D, Е, F имеют, соответственно, десятичные веса 10, 11, 12, 13, 14, 15.
Пример. 11012 = 1 * 23 + 1 * 22 + 0 * 21 + 1 * 20 = 8 + 4 + 1 = 1310,
1578 = 1 * 82 + 5 * 81 + 7 * 80 = 64 + 40 + 7 = 11110,
A6F16 = 10 * 162 + 6 * 161 + 15 * 1 = 267110.
Для изображения десятичных дробей используется формула разложения по степеням основания.
Пример. 110.0012 = 1*22 + 1 * 21 + 0 * 20 + 0 * 2-1 + 0 * 2-2 + 1 * 2-3 = 6.12510;
A.B16 = A * 160 + B * 16-1 = 10 * 1 + 11 * 0,0625 = 10,687510.
Процедура перевода десятичных чисел в систему счисления Р:
1. Перевести отдельно целую часть числа х, для чего последовательно делить сперва целую часть [х]10, а затем все частные (получаемые при делении) на р до тех пор, пока не получим в очередном частном число меньшее р; изображение [х]p получается последовательным приписыванием к последнему частному остатков от деления – от последнего до первого;
2. Перевести отдельно дробную часть (мантиссу) числа, то есть {x}10, для чего последовательно умножать сначала исходную мантиссу, а затем мантиссы получаемых чисел на р до тех пор, пока не получим мантиссу, равную нулю, или нужное количество цифр в {х}p; изображение {х}p получается приписыванием к целой части первого произведения второй такой же цифры и т.д., до последней цифры целой части;
3. результат будет иметь вид (х)р = [х]p, {х}p.
Пример. Найти: 1210 = ?2. Решение:
1210 = 8 + 4 = 1 * 23 + 1 * 22 + 0 * 21 + 0 * 20 = 11002.
Пример. Найти 2910 = ?8.
Решение имеет вид: 2910 = 3 * 81 + 5 * 80 = 358;
Пример. Найти 7910 = ?16.
Решение: 7910 = 4 * 161 + 15 * 160 = 4F16.
Для перевода из 2-ой в 8-ую системы счислений и наоборот, из 2-ной в 16-ную системы счислений и наоборот, из 8-ной в 16-ную и обратно используется таблица следующего вида:
| ОСНОВАНИЕ СИСТЕМЫ | |||
При переводе в 8-ную систему или из нее необходимо группировать в тройки биты, а при переводе в 16-ную или из нее – группировать их в четверки битов. Можно добавлять, если нужно, незначащие нули (слева от целой части и справа от мантиссы, т.е.дробной части) или отбрасывать их.
Пример. Рассмотрим переводы в смешанных системах.
1. Из 2-ной системы в 8-ную (двоично-восьмеричное изображение):

2. из 8-ной системы в 2–ную (восьмерично-двоичное изображение):
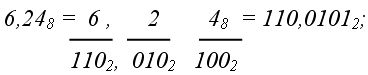
3. из 2-ной системы в 16-ную (двоично-шестнадцатеричное изображение):

4. из 16-ной системы в 2-ную (шестнадцатерично-двоичное изображение):

Сложение в двоичной системе счисления осуществляется по правилам
0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 210 = 102 (единица идет в старший разряд).
Таблица вычитания в двоичной системе счисления имеет вид
0 – 0 = 0, 1 – 0 = 1, 1 – 1 = 0, 0 – 1 = 10 – 1 = 1 (единицу забираем у старшего разряда).
Таблица умножения в двоичной системе счисления имеет вид
0 x 0 = 0, 0 x 1 = 0, 1 x 0 = 0, 1 x 1 = 1.
Таблица деления в двоичной системе счисления имеет вид
0 : 0 = не определено, 1 : 0 = не определено, 0 : 1 = 0, 1 : 1 = 1.
Обратным кодом числа в системе с основанием р называется число в этой системе, получаемое заменой цифры, символа в каждом разряде числа на его дополнение до максимальной цифры в системе (то есть до р – 1).
Дополнительный код = обратный код + единица в младшем разряде.
Пример.
1. 10011  двоичное число,
двоичное число,
01100  обратный код этого двоичного числа,
обратный код этого двоичного числа,
01101  дополнительный код этого двоичного числа;
дополнительный код этого двоичного числа;
2. 457  восьмеричное число,
восьмеричное число,
320  обратный код этого восьмеричного числа,
обратный код этого восьмеричного числа,
321  дополнительный код;
дополнительный код;
3. А9  шестнадцатеричное число,
шестнадцатеричное число,
56  обратный код этого шестнадцатиричного числа,
обратный код этого шестнадцатиричного числа,
57  дополнительный код.
дополнительный код.
Вычитание в ЭВМ идет с помощью дополнительного кода: найти дополнительный код вычитаемого такой же разрядности, как и уменьшаемое, и сложить этот код с уменьшаемым. Результатом вычитания будет полученная сумма без учета старшего разряда, который отбрасывается.
Пример. Выполним вычитание напрямую и через сложение (через дополнительный код):


Нужно всегда иметь в виду, что точность в теоретической математике – понятие абстрактное, и в практической математике может возникать иллюзия точности там, где ее на самом деле нет.
Так как диапазон n-разрядных чисел системы счисления с основанием p находится в пределах  , то для представления дробных чисел этот диапазон еще снижается, поскольку часть разрядов необходимо отвести под изображение мантиссы. Таким образом, имеются так называемые "зоны нечувствительности" форм представления чисел в n-разрядных арифметиках.
, то для представления дробных чисел этот диапазон еще снижается, поскольку часть разрядов необходимо отвести под изображение мантиссы. Таким образом, имеются так называемые "зоны нечувствительности" форм представления чисел в n-разрядных арифметиках.
В 1937 году Конрадом Цузе для увеличения диапазона чисел, представимых в арифметике двоичных чисел, а также для повышения точности этого представления чисел было предложено представление чисел в плавающей, нормализованной форме – число x представляется в виде:  , где m – мантисса числа, k – целый порядок числа,
, где m – мантисса числа, k – целый порядок числа,  .
.
Если из n разрядов, отводимых под изображение чисел, m двоичных разрядов отвести под мантиссу, k – под порядок, один разряд – под знак числа и один разряд – под знак порядка (например, 0 – плюс, 1 – минус), то диапазон представимых в форме с плавающей запятой чисел резко увеличивается (m + k + 2 = n):

(многоточие соответствует k единицам).
Числа, меньшие нижней границы положительных чисел и большие верхней границы отрицательных чисел, считаются равными нулю, не различаются между собой. Числа, большие верхней границы положительных чисел, полагаются равными положительной бесконечности (меньшие нижней границы отрицательных – отрицательной бесконечности).