Акустические волны. Связь между давлением, плотностью, скоростью и смещением частиц воздуха в волне. Интенсивность акустической волны.

Звуковые (акустические) волны - упругие волны в воздухе, частоты которых лежат в пределах от 20 до 20 000 колебаний в секунду.

Ж и газы обладают только объёмной упругостью. В них возможны только продольные волны.

Рассмотрим участок газа, сечения s, длины dx.

 

 

r₀ s dx ¶²S/¶t² = [P_x – P_x+dx] s

r₀ ¶²S/¶t² = - ¶P/¶x

При малых изменениях давления у положения p₀:

dP=(¶P/¶r)_r0 dp=c² dr

-¶P/¶x=-c² ¶dr/¶x=–c² ¶/¶x[r₀ (-¶S/¶x)]=c²r_o ¶²S/¶x²

¶²S/¶t² = c² ¶²S/¶x² , c²= ¶P/¶r, при r=r₀

Зависимость от температуры:

P=rRT/m P=const r^g g=С_р/С_V dP/dr= g const r^g-1= g P₀/r₀ Þ

Þ C²=g P₀/r₀= g RT/m

 

Пусть плоская акустическая волна возбуждается бесконечной пластинкой, колеблющейся в направлении x по закону .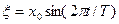

Тогда волна распространяется также в направлении x, смещение частиц, лежащих в любой плоскости, нормальной к этому направлению, происходит по з-ну: .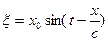

Относительное изменение толщины слоя, лежащего между двумя бесконечно близкими пл-тями: .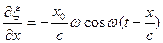

Этому изменению расстояния соответствует такое же относительное изменение обьема, заключенного между двумя пл-тями. 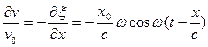(5)

Скорость частиц: 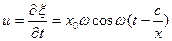. (6)

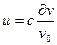Из (5) и (6) Þ (7)

dv/v₀=–dr/r₀ (8)

dp/dr=g p₀/r₀

Из (8),(9) Þ Dp=g p Dr /r =g pu/c=r cu, т.к. (1). (10)

Интенсивность.Звуковая волна несет с собой потенциальную энергию - энергию упругой деформации газа и кинетическую энергию движущихся частиц газа. Подсчитает потенциальную энергию, заключенную в элементе обьема SDx. Если относительное сжатие в слое есть h=dv/v₀, то по (10) сила, действующая на стенку площади S, есть SDp=ghp. При изменении относительного сжатия на dh стенка перемещается на Dx× dh и при этом совершается работа dA=S×Dx×gp×h×dh.

u=SDxg p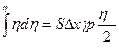

Плотность энергии упругой деформации w_U=gph²/2 (14)

Кинетическая энергия этого же обьема T=r SDxu²/2 и плотность кинетической энергии w_T=ru²/2. Из (7) видно, что w_U=w_T. Тогда плотность всей энергии звуковой волны w=gp×h². Т.к. h меняется как cos, то h² меняется как cos², значит h²_ср=h₀²/2, w_ср=g ph₀²/2. Т.к. (7) выполняется для всяких мгновенных значений Dз и h, то оно справедливо и для амплитудных значений и Þ w_ср=(Dp₀)²c/2g p, где Dp₀ - амплитуда звукового давления.

Энергия, которая падает за единицу времени на единицу площади, нормальной к направлению распространения звуковой волны, называется интенсивностью звуковой волны.

Интенсивность звука I=w_ср c=(Dp₀)²c/2g p==(Dp₀)²/2r c (т. к. с²=g p/r)

Интенсивность звука измеряется в дж/см²×с.