Группы и их свойства. Примеры
Определение 1. 2. 1.Моноид < А, ∙> называется группой, если каждый элемент из А симметризуем.
Это наиболее распространённое и естественное современное определение группы. Выпишем данное определение группы более подробно:
Определение 1. 2. 2. Группой называется множество А с заданной на нем бинарной алгебраической операцией, удовлетворяющей следующим трём аксиомам (используем мультипликативную форму записи):
А1. ( 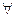 а, b, с
а, b, с 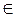 А) (а ∙ b)∙ с = а ∙(b ∙ с) (ассоциативность),
А) (а ∙ b)∙ с = а ∙(b ∙ с) (ассоциативность),
А2. (  1
1 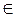 A)(
A)( 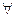 а
а 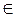 А) а ∙ 1 = 1 ∙ а = а (наличие единицы),
А) а ∙ 1 = 1 ∙ а = а (наличие единицы),
A3. ( 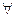 а
а 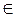 А) (
А) (  а'
а' 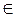 А) а ∙ а' = а'∙ а = 1 (обратимость элементов), где 1- единица из А; её существование обеспечивается аксиомой 2 и, как мы уже знаем, она единственна.
А) а ∙ а' = а'∙ а = 1 (обратимость элементов), где 1- единица из А; её существование обеспечивается аксиомой 2 и, как мы уже знаем, она единственна.
Замечание.Для доказательства того, что множество А с операцией * является группой, нужно:
1) показать, что операция * является бинарной операцией на множестве А, т.е. выполнимой и однозначной операцией ранга2 (в операции участвуют 2 элемента из А: (а, b) 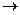 а * b);
а * b);
2) проверить выполнимость аксиом A1, А2, А3.
Если первое из этих условий не выполняется, то нет смысла в проверке аксиом.
Примеры групп:
1. Покажем, что < Z, + > - группа:
операция “+” является выполнимой на Z, так как ( 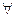 а, b
а, b 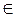 Z) а + b
Z) а + b 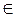 Z; однозначной на Z, так как результат (а + b) определяется однозначно; ранг операции равен 2, так как в операции используется два элемента (a, b)
Z; однозначной на Z, так как результат (а + b) определяется однозначно; ранг операции равен 2, так как в операции используется два элемента (a, b)  а+ b (следовательно, < Z, + > - группоид);
а+ b (следовательно, < Z, + > - группоид);
А1 выполняется, так как сложение целых чисел ассоциативно:
( 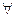 а, b, с
а, b, с 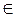 Z) (а+ b) + с = а + (b+ с), следовательно, < Z, + > - полугруппа;
Z) (а+ b) + с = а + (b+ с), следовательно, < Z, + > - полугруппа;
А2 выполняется: роль нейтрального элемента будет играть число 0, так как ( 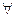 а
а  Z) а + 0 = 0 + а = а, следовательно, <Z, +> – моноид;
Z) а + 0 = 0 + а = а, следовательно, <Z, +> – моноид;
А3 выполняется: для всякого целого числа существует противоположное число (  а
а  Z) (
Z) (  – а
– а  Z) а + (– а) = (– а) + а = 0 , следовательно, < Z, + > – группа.
Z) а + (– а) = (– а) + а = 0 , следовательно, < Z, + > – группа.
2. < А, + >, где А = п× Z, или А = Q , или А = R, или А = С; п - неотрицательное целое число.
3. < А, × >, где А = Q*, или А = R* или С*, или А= Q+, или А= R+;
Q*(Q+) - множество всех ненулевых (положительных) рациональных чисел, R* (R+) - множество всех ненулевых (положительных) действительных чисел, С* - множество всех ненулевых комплексных чисел.
4. < А, × >, где А = {1}, или А = {1, – 1}, или А= {1, –1, i, – i}.
5. Множество всех матриц одинаковой размерности с действительными элементами относительно операции сложения матриц.
6. Множество всех невырожденных квадратных матриц одинакового
порядка с действительными элементами относительно операции умножения матриц.
7. Множество всех биекций, т. е. взаимно однозначных отображений некоторого множества М на М с операцией композиции отображений.
8. Множество всех симметрии (самосовмещений) геометрической фигуры ни плоскости или в пространстве с операцией последовательного выполнения самосовмещений.
Рассмотрим подробнее группу G  = {е, а, а2, b, а × b, а2× b} симметрий правильного треугольника, где а – поворот на 120° вокруг центра правильного треугольника против часовой стрелки, b - осевая симметрия относительно вертикальной оси, проходящей через высоту треугольника (Рис. 1).
= {е, а, а2, b, а × b, а2× b} симметрий правильного треугольника, где а – поворот на 120° вокруг центра правильного треугольника против часовой стрелки, b - осевая симметрия относительно вертикальной оси, проходящей через высоту треугольника (Рис. 1).
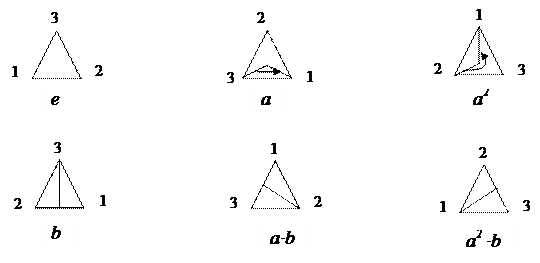 |
Рис. 1
Тогда а3 = b2 = е (е - тождественное самосовмещение треугольника).
b × а = а × b (где b × а - композиция отображений; последовательно выполняется вначале отображение а, затем – b).
9. Множество С[х] всех многочленов от одного неизвестного с комплексными коэффициентами относительно операции сложения многочленов.
10. Множество всех непрерывных числовых функций относительно операции поточечного сложения функций.
11. Множество всех непрерывных, не обращающихся в нуль числовых функций относительно операции поточечного умножения функций.
12. Для n 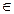 N множество Zn = {0,1, 2, ..., n - 1} с операцией а
N множество Zn = {0,1, 2, ..., n - 1} с операцией а  b = с, где с - остаток отделения а + b на с.
b = с, где с - остаток отделения а + b на с.
Как показывают примеры, группы бывают как конечные, так и бесконечные.
Определение 1. 2. 3.Число элементов конечной группы А называется её порядком и обозначается | А |.
Все группы можно разделить также на коммутативные или абелевы (в честь норвежского математика Хенрика Абеля) и некоммутативные.
Определение 1. 2. 4.Группа < А,∙>называется абелевой (коммутативной), если (  а, b
а, b  А) а × b = b × а.
А) а × b = b × а.
Перечислим ряд важнейших исходных свойств групп, непосредственно вытекающих из аксиом.
Свойства групп
Для произвольной группы < А, ×> имеем:
(1) в А существует единственная единица 1.
(2) для каждого а  А существует однозначно определенный обратный элемент а
А существует однозначно определенный обратный элемент а  А.
А.
(3) в А однозначно разрешимы уравнения а × х = b и у × а = b для любых двух элементов а и b из А, именно, х = а-1 × b и y = b × а-1 .
(4) справедливы законы сокращения: а × b= а × свлечёт b = си а× с = b× с влечёт а = b для любых а, b, с из А.
(5) в А имеет место обобщённый закон ассоциативности, а в случае абелевой группы - обобщённый закон коммутативности.
(6) (а-1)-1 = а для всех а  А.
А.
(7) (а1 × а 2 × …× а n)-1 = аn-1 × … × а1-1 для любого конечного числа п элементов а1, ... , аn группы А. В частности, (an) - 1 = (a - 1)n.
(8) в А можно определить степень а произвольного элемента а  А с произвольным целым показателем k:
А с произвольным целым показателем k:
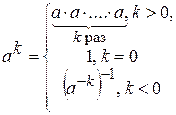
(9) в группе А можно определить операции деления: правое (а / b = а × b-1) и левое (а \ b = b-1 × а), при этом элементы а × b-1 и b-1 × а называют правым и левым частным элементов а и b соответственно.
Замечание.Для абелевой группы А обе операции деления совпадают.