Медленные и быстрые замирания сигналов в радиоканале. Методы их оценки

Как уже было показано, при перемещении подвижного объекта (ПО) наблюдаются быстрые флуктуации параметров сигнала вследствие частотно-временной дисперсии передаточной функции канала передачи, вызванной его многолучевостью [5].

Флуктуации начальной фазы сигнала в точке приема определяются изменением его местоположения, а при движении объекта являются функцией времени. Кроме того, при движении объекта из-за доплеровского эффекта наблюдается случайная частотная модуляция, характеристики спектра которой зависят от скорости объекта, а также других факторов. Таким образом, канал передачи является частотно-селективным. Кроме того, случайные задержки приходящих в точку приема копий сигнала приводят к возникновению временной селективности канала передачи и вызванных ею гладких флуктуации амплитуды суммарного сигнала в точке приема.

Существует несколько функций распределения вероятности, которые используются для моделирования статистических характеристик каналов с замираниями. Если в среде распространения сигнала присутствует множество рассеивателей, каждый из которых вносит свой вклад в величину принимаемого сигнала (как в случае ионосферного или тропосферного распространения), то применение центральной предельной теоремы приводит к гауссовской модели импульсной характеристики канала. Если процесс имеет нулевое математическое ожидание, то огибающая импульсной характеристики радиоканала в любой момент времени имеет релеевское распределение, а фаза импульсной характеристики имеет равномерное распределение в интервале [0, 2 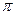]. Для оценки статистических параметров радиоканалов с замираниями и многолучевостью, наряду с распределениями Релея и Райса, используют распределение Накагами [40].

Медленные замирания сигнала обусловлены эффектом тени, который вызывают препятствия, и возникают при перемещении мобильных абонентов на значительные расстояния (> 10 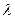.) [24]. В ходе таких перемещений трасса распространения сигнала между БС и МС успевает значительно измениться: на пути радиоволн возникают новые препятствия, основные лучи приходят к МС по другим маршрутам. Соответственно изменяются и мгновенные значения уровня сигнала на входе приемника МС.

Медленные замирания зависят от макроструктуры канала связи, их параметры во многом определяются типом застройки, рельефом местности, видом растительности, скоростью мобильного абонента и т.п. Медленные замирания часто моделируют логарифмически нормальным законом распределения мгновенных значений огибающей принимаемого сигнала [5, 61:

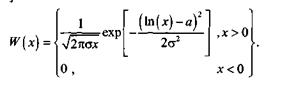(7.8)

где х – значение огибающей сигнала; а и 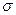– параметры распределения. Как правило, в крупных городах интенсивность медленных замираний 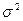составляет порядка 10 дБ, в пригородах – 6 дБ, а периодичность замираний соответствует перемещению МС на десятки метров. Фактически, медленные замирания представляют собой изменение среднего уровня сигнала, на которые накладываются быстрые замирания вследствие многолучевого распространения.

Преодолев расстояние от БС до МС, один или несколько основных лучей приходят в локальную зону приема МС (радиус локальной зоны, как правило, десятки метров). Далее происходит рассеяние энергии сигналов основных лучей на многочисленных рассеивателях, расположенных в локальной зоне (это могут быть стены зданий, автомобили, рекламные щиты и прочие объекты, способные отражать и рассеивать радиоволны). В результате на МС приходит большое число микросигналов с различными амплитудами, задержками, начальными фазами и допплеровскими частотными сдвигами. Интерферируя в точке приема, эти сигналы вызывают быстрые замирания огибающей суммарного сигнала [6]. Глубина быстрых замираний может достигать 10...30 дБ, и приводить к ослаблению основного сигнала. Помимо глубины, быстрые флуктуации сигналов принято характеризовать скоростью и средней длительностью замираний. При перемещении МС периодичность пространственных флуктуации составляет около полуволны (порядка 10... 15 см в линейной мере). Период флуктуации во времени зависит от скорости перемещения МС: например, при скорости 50 км/ч период флуктуации составляет около 10 мс, а частота замираний глубиной 10.. .30 дБ составляет 5-50 провалов в секунду при средней длительности замираний порядка 0,2.. .2 мс.

В городских условиях при глубинах замираний до 20 дБ экспериментально наблюдается хорошее согласование статистики флуктуации с релеевским законом распределения. Более глубокие замирания соответствуют закону Раиса, что говорит о наличии в сигнале слабой регулярной компоненты. Результаты многочисленных экспериментов [5] говорят о том, что общепринятая модель флуктуации амплитуды сигнала по закону Релея для многих случаев неадекватна. Это объясняется следующими факторами:

- неравномерным угловым распределением по азимуту направлений прихода сигнала;

- наличием в угломестной плоскости отличного от нуля спектра углов прихода сигнала;

- значительным разбросом моментов прихода отражённых сигналов;

- значительной разницей величин мощности отражённых сигналов.

В [5] автор описывает развитие данной модели, в которой предполагается корреляция между нормально распределенными квадратурными составляющими амплитуды сигнала. Физически это явление объясняется возможностью экранирования лучей, отраженных от окружающих МС предметов из некоторого сектора углов прихода. Исследование влияния такого эффекта показало его умеренную значимость, которой можно пренебречь в инженер-яой практике. Кроме того, значение коэффициента корреляции при перемещении МС не-арерывно меняется и в получаемых натурных экспериментальных результатах усредняется. В другом примере развития данной модели все отражённые копии сигнала разбиваются на кластеры, в пределах которых удовлетворяются условия формирования релеевских замираний. Таким образом, принимаемый сигнал представляется суммой парциальных сигналов, флуктуирующих по закону Релея. Если число парциальных сигналов стремится к бесконечности, а их мощности близки, то получается аппроксимация Джейкса [47].

Глубокие замирания амплитуды вызывают скачки фазы сигнала и соответствующие им, близкие к дельта-функции, всплески случайной частоты, являющейся производной от случайной фазы. Таким образом, для одночастотного сигнала многолучевость приводит к флуктуации фазы сигнала в точке приема, связанным с нею глубоким замираниям амплитуды сигнала и случайной частотной модуляции, обусловливающими неустранимую ошибку при использовании угловых методов модуляции.

Скорость замираний есть число пересечений огибающей некоторого уровня (например 3 дБ) в единицу времени. Средняя длительность замираний – это средняя длительность интервала времени, в течение которого огибающая сигнала находится ниже определенного уровня. Распределение мгновенных значений огибающей быстро замирающего сигнала часто описывают законом Релея-Райса [70].

Если МС находится вне зоны прямой радиовидимости БС, прямой луч отсутствует и в принятом сигнале нет незамирающей компоненты. Распределение Релея-Раиса в этом случае сводится к чисто-релеевскому распределению.

return false">ссылка скрыта

При появлении прямого луча и с ростом энергии незамирающей компоненты распределение Релея-Райса трансформируется в гауссовское. В пределе, когда отношение энергии сигнала, пришедшего по прямому лучу (без замираний) к суммарной энергии рассеянья сигналов стремится к бесконечности, распределение Релея-Райса вырождается в 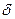-функцию: W(x) = 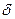(х – s), где s – значение огибающей сигнала, пришедшего по прямому лучу (полная детерминированность).

Средний интервал быстрых замираний при движении МС приблизительно равен половине длины волны. Затухание сигнала на трассе распространения, а также эффекты медленных и быстрых замираний в совокупности определяют энергетические соотношения в канале связи [6] (см. рис. 7.3).

Передатчик БС генерирует сигнал мощностью Рпрд, который через комбайнер и фидер направляется к антенне БС с коэффициентом направленного действия GБС. В канале связи сигнал затухает по мощности на величину Lpl дБ и, испытывая медленные (Lsl) и быстрые (Lfs) замирания, приходит к антенне МС с коэффициентом направленного действия G а затем поступает на вход линейного тракта приемника (ЛТП) МС с чувствительностью равной Р .

Рис. 7.3. Энергетические соотношения в канале связи

Для того, чтобы вероятность ошибки при приеме символа сообщения находилась в заданных пределах

(1...2%), вводят запас мощности передатчика БС на медленные и быстрые замирания. На рис. 7.3 вероятность ошибки 1...2% численно равна заштрихованным площадям под кривыми вероятностей распределения огибающих.

В экстремальном случае, когда медленная и быстрая составляющие замираний действуют синфазно и огибающая принимаемого сигнала становится ниже допустимого уровня, полезный сигнал почти полностью «тонет» в шумах и вероятность ошибки при приеме символа приближается к 0,5. Запас мощности передатчика БС на замирания (Lsl + Lp) выбирают таким образом, чтобы вероятность ошибки на бит на выходе приемного тракта МС не превышала ■ допустимой величины (обычно 10 ... 10 ) с учетом корректирующей способности кодов. В итоге мощность передатчика БС составляет:

Р = Lpl + Lsl + Lfs + Lc/f- GBS – GMS + Рпрм.ср [дБ], Рпрд > Po, (7.9)

где Lc/f— потери мощности в комбайнере и фидере БС, а Pпрм.ср – требуемая средняя мощность сигнала на входе линейного тракта приемника МС.

Величина средних потерь на трассе распространения и параметры медленных и быстрых замираний еще не дают исчерпывающего описания канала связи. Известно [6], что частотно-временные сдвиги сигналов в канале связи вызывают селективные замирания по времени и частоте, значительно усложняющие работу современных цифровых систем мобильной связи с высокоскоростной передачей информации.

Многолучевое распространение сигналов, при котором каждый луч приходит со своим временным сдвигом, приводит к растяжению принимаемых символов во времени и частотно-селективным замираниям. Растяжение во времени проявляется в том, что длительность принятых символов больше, чем длительность переданных. При этом соседние символы сообщения могут перекрывать друг друга.

Частотно-селективные замирания сигнала эквивалентны фильтрации сигнала, при которой различные компоненты спектра сигнала получают разное ослабление. Спектральные составляющие в пределах малого интервала частот будут испытывать приблизительно одинаковое ослабление (гладкие замирания), но с ростом частотного разнесения характер замираний станет существенно различным. Очевидно, что чем больше ширина полосы сигнала, тем более он будет подвержен частотно-селективным замираниям.

Считается [21], что минимальная ширина полосы, при которой приемник способен обнаружить временное растяжение символов, составляет 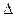Fmin = 1/4 , где – разность временных сдвигов сигналов в первом и последнем пришедшем лучах.

При достаточно большой ширине полосы сигнала приемник способен различать лучи с различными временными задержками. Это происходит, когда разрешающая способность приемника по времени становится меньше взаимного временного сдвига сигналов в i-м и j-м лучах: < ( – ).

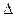Для простоты можно считать, что разрешающая способность приемника равна длительности элементарного символа и обратно пропорциональна ширине полосы сигнала: = = 1/ F.

Когда максимальный временной сдвиг сигналов в разных лучах превышает длительность символа

(max | – | > ), соседние символы принимаемого сигнала полностью перекрывают (маскируют) друг друга. В этом случае говорят о явлении межсимвольной интерференции (МСИ).

Частотно-селективные замирания приводят к искажениям формы спектра сигнала и, как следствие, к искажениям формы переданных символов. Эти искажения начинают проявляться, когда ширина полосы передаваемого сигнала превышает полосу когерентности канала связи. 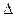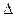Полосой когерентности Bc(t) называют такой интервал частот, замирания спектральных компонентов на границах которого характеризуются определенным значением коэффициента корреляции ( f, t).

Допустимые искажения, при которых система обеспечивает заданное качество связи, соответствуют различным значениям коэффициента корреляции и зависят от методов обработки сигналов в кодеке и модеме. Отдельные системы могут испытывать сбои в работе, когда ширина полосы сигнала такова, что ( 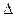f, 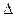t) = 0,9, тогда как использование сложных адаптивных методов обработки позволяет обеспечить требуемые характеристики при

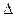( f, 0)= 0,37 [24].

Там же показано, что при определенных статистических допущениях,

(7.11)

где 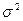– дисперсия многолучевого растяжения сигнала в канале связи.

Если принять пороговое значение коэффициента корреляции равным 0,5, полоса когерентности канала связи составит:

(7.12)

Так, при типичной для города стандартной девиации многолучевого растяжения 2 мкс полоса когерентности канала связи составляет 80 кГц. Сигналы с большей шириной полосы будут подвержены частотно-селективным замираниям и межсимвольной интерференции.

При изменении характеристик канала связи с течением времени говорят о временных селективных замираниях. Временные селективные замирания вызывают искажения формы посылок передаваемых сообщений, поскольку характеристики канала связи существенно изменяются за время прохождения сигнала по трассе БС-МС. Причиной изменения коэффициента передачи канала мобильной связи могут быть допплеровские частотные сдвиги: они приводят к растяжению спектра частот сигналов и вызывают временные селективные замирания.

В приложении 2 представлены основные модели прогнозирования потерь на трассе распространения сигнала для расчета зон радиопокрытия сетей подвижной связи.