Амплитудно-частотный спектр

 

Огибающая АЧС последовательности прямоугольных видеоим­пульсов описывается функцией

.

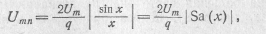
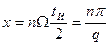и пересекает ось частот, когда х кратно л, т. е. п кратно q, τ. е. при частотах, кратных скважности. Поэтому именно эти частоты, равные

отсутствуют в спектре.

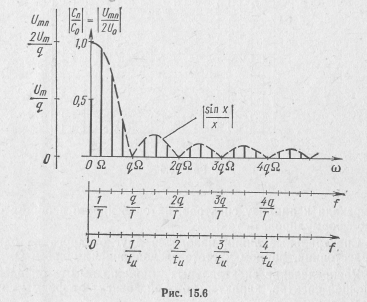
Обычно при построении спектров откладывают относительные

величины, т. е. 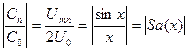и получают

относительный или нормированный спектр (рис. 15.6).

Спектральные составляющие с наибольшей амплитудой распо­ложены под первыми арками, в них сосредоточена и основная часть энергии сигнала. Поэтому эффективную ширину спектра можно определить как

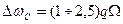. (15.26)

Теоретически ширина спектра бесконечна, однако не все его составляющие оказывают действенное влияние на форму сигнала и имеют практическое значение. Поэтому под шириной спектра обычно понимают ограниченный диапазон частот, внутри которого распределена большая часть энергии сигнала. Ширина спектра, так же как, например, полоса пропускания контура,— понятие условное.

Рассмотрим особенности АЧС при изменении длительности и частоты следования импульсов (рис, 15.7).

С уменьшением частоты следования Ω при t_И=const происхо­дит сгущение спектра: расстояние между спектральными линиями уменьшается. Ширина спектра, определяемая его огибающей, не

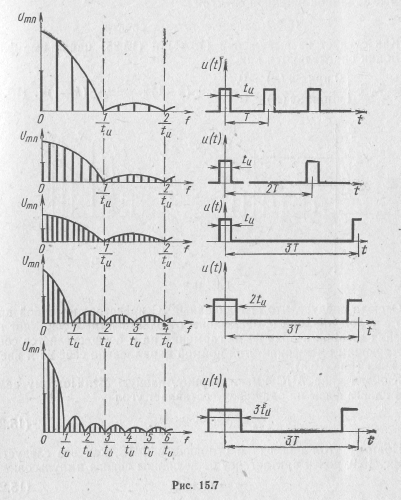
меняется, а основная часть энергии распределяется на большем числе гармоник.

С увеличением длительности импульсов при Ω=const ширина арок и связанная с ней ширина спектра уменьшаются: происходит относительное сжатие спектра. Основная часть энергии распреде­ляется на меньшем числе гармоник и сосредоточивается в области все более низких частот.

Таким образом, чем короче импульсы и больше их скважность, тем шире и гуще их спектр, и наоборот,

На практике часто приходится учитывать в спектре лишь ко­нечное число гармоник. Точность аппроксимации исходной функ­ции в этом случае зависит от числа учтенных гармоник. Она ока­зывается достаточной, если учитываются все гармоники, опреде­ляемые заданной шириной спектра.

 

15.3.2. Фазо-частотный спектр

 

Как следует из выражений (15.24) и (15.25) начальные фазы гармоник определяются как

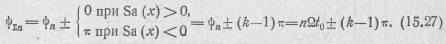
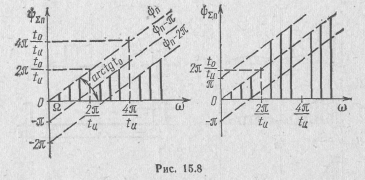
Отсюда следует, что огибающая ФЧС представляет собой пря­мую с углом наклона α, зависящим от сдвига импульсов. Учет из­менения от арки к арке фазы гармоник на я осуществляется соот­ветствующим смещением этой прямой параллельно себе на π вверх или вниз (рис. 15.8).

Каждая арка АЧС имеет ширину, равную qΩ. Поэтому вели­чина сдвига фазы на одну арку составляет угол

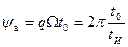. (15.28)

Поэтому угол наклона α огибающей ФЧС, как это следует и из рис. 15.9, равен арктангенсу от величины сдвига импульсов:

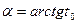. (15.29)

Чем больше сдвиг импульсов во времени, тем больше наклон огибающей их ФЧС (рис. 15.9). При t₀=0 угол α равен нулю.

Симметричные частотные спектры имеют аналогичный вид, но построение спектральных линий на них распространяется на ось отрицательных частот. При этом АЧС и ФЧС оказываются симмет­ричными относительно оси ординат и начала отсчета соответ­ственно (рис. 15.10).

 

Пример15.1.

Рассчитать спектры периодической последовательности прямоугольных видео­импульсов, если U_m = 10O мВ; q=5; 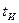=0,02 мс; t₀=2 t_И.

Решение.

1. Расстояние между спектральными линиями, равное частоте следования импульсов

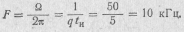
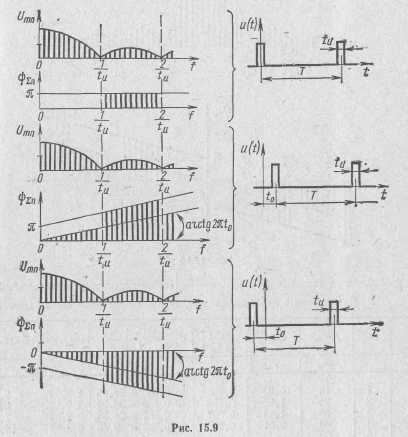
2. Ширина арки:

.

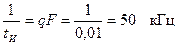3. Количество спектральных линий под каждой аркой:

.

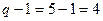4. Сдвиг фазы на одну арку:

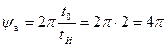5.

Постоянная составляющая:

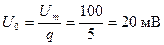
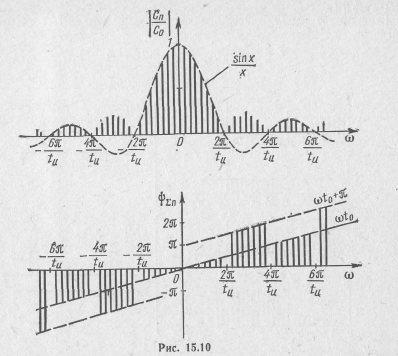
6. Табличные значения функции 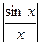соответствующие частотам F, 2F, 3F.....и рассчитанные с их помощью амплитуды и начальные фазы гармоник:

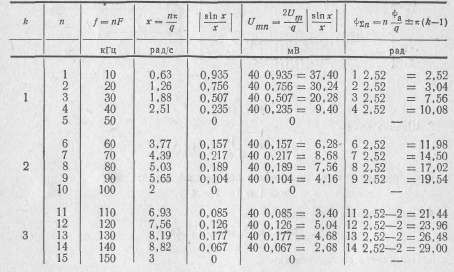
В спектре отсутствуют гармоники, кратные q=5, т. е. 5F=50 кГц, lOF= 100 кГц, 15F=150 кГц и т. д.

15.4. СПЕКТРЫ ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ

ПРЯМОУГОЛЬНЫХ РАДИОИМПУЛЬСОВ

 

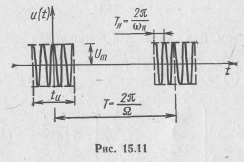
Рассчитаем спектр симметричной относительно оси ординат последовательности прямоугольных радиоимпульсов (рис. 15.11):

Здесь 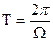и Ω— период и частота следования импульсов;

ω_H — несущая частота.

Если несущая частота кратна частоте следования, т. е. ω_H=kΩ, где k — целое число, то импульсы называются когерентными, если эти частоты некратны ( 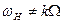), то импульсы — некогерентные.

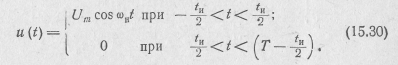
С помощью выражения (15.4) находим постоянную состав­ляющую

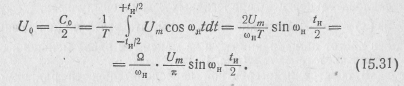
В силу симметрии функции относительно оси ординат ряд Фурье будет содержать лишь косинусоиды (b_n = 0)..

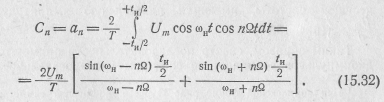
Отсюда следует, что амплитуды гармонических составляющих резко возрастают в районе значений частот, близких к ω_н, т. е. .По в этом районе значений п второе слагаемое в выра-

Жении (15.32) значительно меньше первого, и им можно прене­бречь¹. Кроме того, так как ω_H>Ω, постоянной составляющей можно также практически пренебречь.

Таким образом, при сделанных допущениях

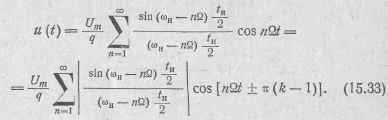
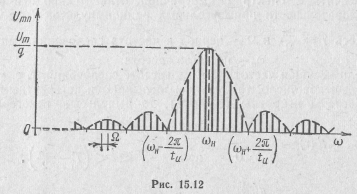
Отсюда следует, что огибающая АЧС последовательности пря­моугольных радиоимпульсов определяется, так же как и для по­следовательности аналогичных видеоимпульсов, функцией 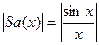. Разница лишь в том, что эта функция сдвинута по оси частот на величину , а ее максимум вдвое меньше и соответ­ствует частоте 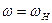. (рис. 15.12).

В спектре некогерентной последовательности радиоимпульсов несущая частота сон отсутствует, и наибольшую ампли­туду имеет составляющая с частотой, близкой к . Если импульсы когерентны, то в их спектре присутствует составляющая несущей частоты, имеющая наибольшую амплитуду, равную 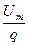(рис. 15.13).

Таким образом, спектр последовательности прямоугольных ра­диоимпульсов совпадает со спектром последовательности прямо-

¹ При комплексной форме ряда Фурье и построении симметричных спек­тров п принимает не только положительные, но и отрицательные значения. При отрицательных п в формуле (15.32) нельзя пренебречь вторым слагаемым, так как в районе частот 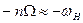, оно становится, наоборот, значительно больше первого слагаемого.

угольных видеоимпульсов, смещенным вправо по оси частот на величину ω_н. При этом часть спектра, лежащая в области ω<ω_н, является зеркальным отображением части спектра, лежащего в области ω> ω_н. Сделанные выводы тем точнее, чем ω_н >Ω,

Наиболее эффективные спектральные составляющие, имеющие наибольшие амплитуды, у радиоимпульсов сосредоточены вблизи несущей частоты. Эффективная ширина спектра радиоимпульсов в два раза больше, чем у одинаковых по длительности видеоим­пульсов.

Пример 15.2.

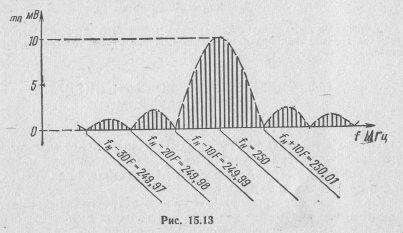
Построить AЧC периодической последовательности прямоугольных радио­импульсов, если U_m = 100 мВ; f_H=250 МГц; 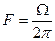кГц; t_И =100 мкс.

Решение.

1. Скважность импульсов:

.

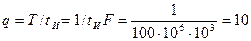2. Ширина малых арок и половины большой арки:

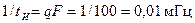
3. Максимальная ордината огибающей спектра:

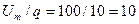мВ.

4. Так как f_H кратно F, импульсы когерентны, основная спектральная со­ставляющая имеет частоту, равную f_H = 250 МГц.

В спектре, показанном на рис. 15.13, присутствуют частоты:

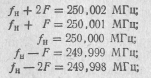
отсутствуют частоты:

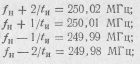
Амплитуды соответствующих гармоник могут быть непосредственно отсчи­таны из графика как ординаты огибающей, взятые при соответствующих ча­стотах.

 

15.5. СВЯЗЬ МЕЖДУ ФОРМОЙ СИГНАЛА И ЕГОСПЕКТРОМ

 

Форма сигнала в полной мере определяется лишь совокупно­стью двух его спектров: АЧС и ФЧС. Тем не менее можно устано­вить ряд характерных связей между формой сигнала и парамет­рами его АЧС, которые позволяют на практике, имея АЧС, судить о форме сигнала, и наоборот.

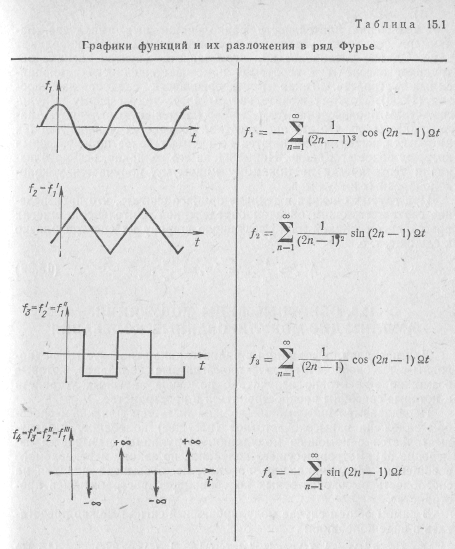
Сравнивая спектры прямоугольных и треугольных импульсов, заметим, что ряд Фурье в случае треугольных импульсов сходится быстрее, чем в случае прямоугольных импульсов, так как ампли­туды гармоник убывают быстрее с ростом их номера (табл. 15.1). Закономерность, по которой уменьшаются амплитуды гармоник с ростом их номера, можно выразить через число раз дифферен­цирования исследуемой функции, необходимое для "выделения из нее дельта-функций. Пусть в k-й производной исследуемой функ­ции появляются дельта-функции. Тогда для коэффициентов Фурье имеют силу неравенства:

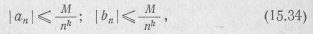
где М — постоянная, зависящая от формы сигнала.

Скорость убывания амплитуд гармоник в спектре зависит от структурных свойств сигнала: коэффициенты убывают тем быст­рее, чем более «гладкой» является форма сигнала и его производ­ных. Если сигнал имеет скачкообразные переходы (его функция имеет конечные разрывы) и в его первой производной появляются δ(t)-импульсы, то амплитуды гармоник в его спектре стремятся к нулю очень медленно — порядок 1/п; если'же в пределах пе­риода следования сигнал непрерывен, но в его первой производ­ной имеются конечные разрывы, а во второй — δ(t)-импульсы, то амплитуды его гармоник стремятся к нулю быстрее—порядок не ниже 1/n² и τ. д. .Чем быстрее убывают коэффициенты Фурье, чем более «гладкая» форма сигнала, тем меньше ширина его спектра. В пределе имеет место наиболее «гладкое» моногармоническое колебание.

Понятие длительности определено лишь для прямоугольных и сходных с ними импульсов. На практике длительность импульса произвольной формы, так же как и ширину спектра сигнала, опре-

деляют энергетическим методом, т. е. как интервал времени, внутри которого -сосредоточена большая часть его энергии, на­пример 90%. Ширина спектра импульсов получается тем больше, чем меньше длительность импульсов. Важным свойством АЧС сиг­нала является то, что произведение длительности импульса на ширину спектра есть величина постоянная для импульсов данной формы:

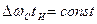. (15.35)

Это свойство присуще спектрам любых сигналов и играет су­щественную роль при выборе их параметров.

Уменьшение длительности радиолокационных импульсов, на­пример, позволяет увеличить точность определения координат цели. Однако увеличение при этом ширины спектра сигнала за­трудняет обеспечение требуемой помехозащищенности радиопри­емных устройств. Такая противоречивость следует из усло­вия (15.35). Поэтому желательно выбирать такую форму импуль­сов, чтобы произведение 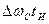имело наименьшую величину. Ана­лиз показывает, что это произведение получается меньше для тех импульсов, которые изменяются во времени более плавно, форма которых более «гладкая». Наименьшая его величина, весьма близ­кая к теоретически достижимому минимуму, получается у коло-колообразных импульсов.

При грубых оценках в технике принято считать, что произведе­ние соответствующим образом определенной длительности многих простейших сигналов на эффективную ширину их" спектра близко к единице, т. е.