Затухающие колебания. Показатель (коэффициэнт) затухания, логарифмический декремент, добротность.

Затухающие колебания.Воспользуемся наиболее простым случаем «жидкого» или «вязкого» трения, когда сила трения направлениа противоположно скорости и пропорциональна скорости. Колебания при наличии трения становятся затухающими:

. - коэффициент трения,

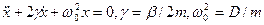
Решение этого уравнения удобно искать в виде

. Учитывая, что ,

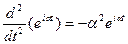, находим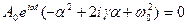

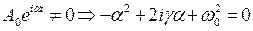
Решение этого уравфнения: 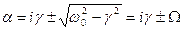, где

, (*)

При не очень больших

- вещественная величина и

- гармоническая функция

Вещественная часть колебания, описываемого равенством (*), представляется формулой:

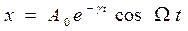
Отсюда видно, что амплитуда колебаний уменьшается
в е=2,7 раза в течение времени

-время затухания, а - показатель (коэффициент, декремент) затухания.

Всё выше написанное относится к случаю не очень больщих коэффициентов трения и когда W – действительное число.