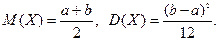А) Биномиальное распределение
Имеется серия из n испытаний, в каждом из которых вероятность наступления события А равна р=Р(А). Случайная величина Х – число наступлений события А. Значения величины Х равны: хi=0, 1, 2, …, n, а вероятности, с которыми появляются значения хi, находятся по формуле  .
.
M(X)=np, D(X)=np(1-p).
В) Пуассоновское распределение
Х – дискретная случайная величина с бесконечным рядом распределения. Значения величины Х равны: хi=0, 1, 2, …, а вероятности, с которыми появляются значения хi, находятся по формуле 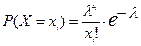 .
.
M(X)=λ, D(X)=λ.
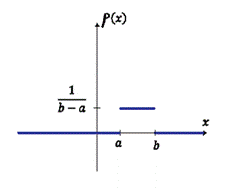
С) Равномерное распределение
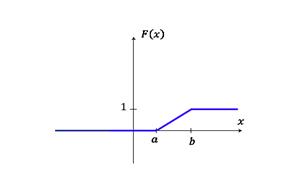
Плотность распределения: Функция распределения:


График плотности распределения: График функции распределения: