Варіант 13
1. За заданими виразами сформувати два вектори – одновимірні масиви Хi та Yj, де і=1..5, а j=1..7

2. За заданим виразом сформувати матрицю O5х9:

3. Обчислити визначник заданої квадратичної матриці:

4. Обчислити транспоновану матрицю до заданої K.
5. Обчислити обернену матрицю до заданої.
6. Обчислити суму заданої та транспонованої матриць.
7. Обчислити добуток заданої та оберненої матриць.
8. Задано число (скаляр). Знайдіть добуток скаляру та заданої матриці K, де скаляр, обчисліть як:
10+№ вашого варіанту, для 1-ї групи;
20+№ вашого варіанту, для 2-ї групи;
30+№ вашого варіанту, для 3-ї групи;
40+№ вашого варіанту, для 4-ї групи.
9. Визначити третій стовпчик заданої матриці K.
10. Обчислити суму елементів визначеного вектора.
11. Знайти максимальний і мінімальний елементи заданої матриці K.
12. Знайти середнє значення елементів матриці.
13. Знайти суму елементів, що розміщені по головній діагоналі у заданій матриці.
14. Визначити кількість рядків та стовпців у заданій матриці K.
15. Створити матрицю з елементів вихідної матриці K, що позначені символом х.
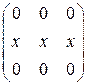
16. Об’єднати вихідну та транспоновану матриці вертикально.
17. Об’єднати вихідну та обернену матриці горизонтально.
18. Обчислити для вихідної матриці K:
· суму елементів другого стовпчика матриці;
· суму двох довільних елементів матриці;
· другу матрицю, кожний елемент якої в п’ять раз більший за відповідний елемент початкової матриці.
19. Відсортувати:
· перший рядок вихідної матриці;
· перший стовпчик транспонованої матриці.
20. Створити одиничну матрицю (n=8).
21. Розв’язати задану систему лінійних алгебраїчних рівнянь (СЛАР) методом Крамера:

та за допомогою вбудованої функції lsolve .