Линейные операции над векторами

Определение 1. Суммой нескольких векторов, например, , называется вектор

по величине и направлению равный замыкающей пространственной ломаной линии, построенной на данных векторах (рис.2).

I. Для двух векторов и их суммой является диагональ параллелограмма, построенного на этих векторах (рис.3).

Так как в треугольнике длина одной стороны не превышает суммы длин других, то

.

II. Для трех векторов их суммой является диагональ параллелепипеда, построенного на этих векторах (рис.4).

Свойства сложения.

1. (коммутативность).

2. (ассоциативность).

3. Для каждого 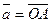существует противоположный вектор , имеющий ту же длину, но противоположное направление (рис.5), и выполняется равенство: .

4. .

Определение 2. Разностью векторов и называется такой вектор , что (рис.6).

Для разности справедливо равенство: .

Определение 3. Произведением вектора на скаляр называется вектор

,

имеющий длину или , направление которого:

1) совпадает с направлением вектора , если ;

2) противоположно ему, если ;

3) произвольно, если .