Свойства бинарных отношений
Бинарные отношения в общем случае обладают свойствами рефлексивности, антирефлексивности, симметричности, антисимметричности, транзитивности, связности.
1. Рефлексивное отношение – отношение  , в котором для любого
, в котором для любого  выполняется
выполняется
 .
.
Другая запись такого отношения  .
.
Главная диагональ матрицы такого отношения содержит только единицы.
Примером рефлексивного отношения является отношение «подобие треугольников, заданное на множестве всех треугольников евклидовой плоскости»: каждый треугольник подобен себе самому;
отношения «  » и «иметь общий делитель».
» и «иметь общий делитель».
2. Антирефлексивное отношение – отношение  , в котором ни для какого
, в котором ни для какого  не выполняется
не выполняется
 или
или  .
.
Главная диагональ матрицы такого отношения содержит только нули.
Примером антирефлексивного отношения является отношение «перпендикулярность прямых, заданных на множестве всех прямых евклидовой плоскости»: никакая прямая не перпендикулярна себе самой;
отношения «<» и «быть сыном».
Отношение «быть симметричным относительно оси  » не является ни рефлексивным, ни антирефлексивным: точка плоскости симметрична сама себе, если она лежит на оси
» не является ни рефлексивным, ни антирефлексивным: точка плоскости симметрична сама себе, если она лежит на оси  и несимметрична сама себе в противном случае.
и несимметрична сама себе в противном случае.
3. Симметричное отношение – отношение  , в котором для пары
, в котором для пары
 из
из  следует
следует  или
или  .
.
Иначе говоря, для любой пары отношение симметричности  выполняется либо в обе стороны, либо не выполняется вообще. Матрица симметричного отношения симметрична относительно главной диагонали:
выполняется либо в обе стороны, либо не выполняется вообще. Матрица симметричного отношения симметрична относительно главной диагонали:  для любых
для любых  и
и  . Для симметричного отношения
. Для симметричного отношения  .
.
Примером симметричного отношения является отношение «быть симметричным относительно оси  », которое является симметричным: если первая точка симметрична второй, то и вторая симметрична первой;
», которое является симметричным: если первая точка симметрична второй, то и вторая симметрична первой;
отношение «проживать в одном доме», заданное на множестве всех жителей некоторого города: если 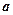 живет в одном доме с
живет в одном доме с  , то
, то  живет в одном доме с
живет в одном доме с 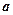 .
.
4. Антисимметричное отношение – отношение  ,в котором для
,в котором для
пары  из
из  и
и  следует, что
следует, что  или
или
 .
.
Примером антисимметричного отношения является отношение «  », заданное на множестве действительных чисел: действительно, если
», заданное на множестве действительных чисел: действительно, если  , и
, и  , то
, то  .
.
5. Транзитивное отношение – отношение  ,в котором для любых
,в котором для любых 
из  и
и  следует
следует  или
или
 .
.
Примером транзитивного отношения являются отношения «равенство», «  », «жить в одном городе»: действительно если
», «жить в одном городе»: действительно если  ; если
; если  ; если
; если 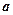 и
и  живут в городе
живут в городе  и
и  и
и  живут в городе
живут в городе  , то
, то 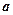 и
и  также живут в городе
также живут в городе  .
.
Отношение «быть сыном» нетранзитивно: если 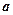 является сыном
является сыном  и
и  является сыном
является сыном  то это не значит, что
то это не значит, что 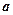 является сыном
является сыном  . Отношение «пересекаться», то есть «иметь непустое пересечение», заданное на системе множеств, также нетранзитивно. Например,
. Отношение «пересекаться», то есть «иметь непустое пересечение», заданное на системе множеств, также нетранзитивно. Например,  пересекается с
пересекается с  ,
,  пересекается с
пересекается с  , однако
, однако  и
и  не пересекаются.
не пересекаются.
Транзитивное замыкание отношения. Транзитивное замыкание отношения  – это отношение
– это отношение  , которое определяется следующим образом:
, которое определяется следующим образом:  , если в
, если в  существует цепочка из
существует цепочка из  элементов
элементов  , в которой между соседними элементами выполнено отношение
, в которой между соседними элементами выполнено отношение  :
:  .
.
Если  транзитивно, то
транзитивно, то  . Действительно, если
. Действительно, если  , то
, то  (цепочка состоит из двух элементов
(цепочка состоит из двух элементов 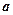 и
и  ), поэтому
), поэтому  . Если же
. Если же  , тосуществует цепочка
, тосуществует цепочка  . Но так как
. Но так как  транзитивно, то
транзитивно, то  , поэтому
, поэтому  . Из включения в обе стороны следует
. Из включения в обе стороны следует  .
.
Транзитивным замыканием отношения «быть сыном» является отношение «быть прямым потомком», являющееся объединением отношений «быть сыном», «быть внуком», «быть правнуком» и т.д.
Транзитивным замыканием отношения «иметь общую стену» для жильцов дома является отношение «жить на одном этаже».
6. Связное (полное) отношение – отношение  , в котором для пары
, в котором для пары 
из  следует
следует  или
или  ,
,
или  .
.
Примером связного (полного) отношения является отношение «быть старше», заданное на множестве родных братьев и сестер некоторой семьи: если  , то либо
, то либо 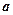 старше
старше  , либо
, либо  старше
старше 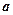 .
.
Рассмотренные свойства можно определить с помощью выражений:
1.  , 2.
, 2.  , 3.
, 3.  , 4.
, 4.  ,
,
5.  (где
(где  – композиция отношений), 6.
– композиция отношений), 6.  .
.
Если даны два отношения  и
и  , то операции над этими отношениями сводятся к операциям над ними, аналогичные операциям над множествами:
, то операции над этими отношениями сводятся к операциям над ними, аналогичные операциям над множествами:
объединению  ; пересечению
; пересечению  ; разности
; разности  ; симметрической разности
; симметрической разности  . Дополнение отношения
. Дополнение отношения  (
(  ) будет равно
) будет равно  .
.
На основании приведенных выше свойств отношений можно дать им ряд определений.
Отношение частичного порядка – отношение, которое рефлексивно, антисимметрично и транзитивно.
Отношение линейного порядка – отношение частичного порядка, которое связно.
Отношение строгого порядка – отношение, которое антирефлексивно, антисимметрично и транзитивно.
Отношение строгого линейного порядка – связное отношение строгого порядка.
В теории множеств важную роль играют два вида специальных бинарных отношений: эквивалентности и порядка, прообразами которых являются понятия равенства, предшествования и предпочтения.