П. 12.3 Прямая в пространстве

Характеристики:направляющий вектор и точка.

Базовая задача:

рис. 2.45

Проведём прямую через точку , параллельно 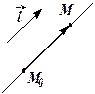данному направляющему вектору 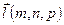. Выберем для этого произвольную точку 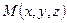, лежащую на прямой . Тогда векторы и 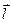коллинеарные. Следовательно, .

Последние равенства называют каноническим уравнением прямой. Из канонического задания прямой можно получить параметрические уравнения прямой: .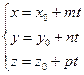

Прямую в пространстве можно рассматривать как пересечение двух плоскостей и .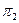

Перейдём к каноническому заданию прямой . Для этого надо задать направляющий вектор 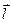и точку 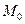, через которую проходит данная прямая. Заметим, что вектор 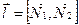(в силу определения векторного произведения). При общем рас положении данных плоскостей они пересекут какую-либо из координатных плоскостей, например, , 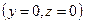. Тогда

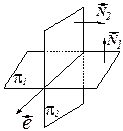
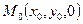- точка пересечения плоскосте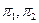й и . Эта точка будет лежать и на прямой . В силу неоднородности выбора точки 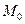обратная задача не ставится.