Теорема 2. Критерий линейной независимости
Для того, чтобы система векторов  была линейно независимой, необходимо и достаточно, чтобы равенство (1) влекло за собой равенство нулю всех
была линейно независимой, необходимо и достаточно, чтобы равенство (1) влекло за собой равенство нулю всех  .
.
Доказательство:
Необходимость.Пусть  ,…,
,…,  линейно независимы. Предположим противное, т.е. что имеет место (1) и из него не следует
линейно независимы. Предположим противное, т.е. что имеет место (1) и из него не следует  . Тогда
. Тогда  , а
, а  . По теореме 1 система
. По теореме 1 система  ,…,
,…,  линейно зависима, что противоречит условию.
линейно зависима, что противоречит условию.
Достаточность.Пусть равенство (1) влечет  . Предположим, противное, т.е.
. Предположим, противное, т.е.  ,…,
,…,  линейно зависимые. Тогда по теореме 1 найдутся
линейно зависимые. Тогда по теореме 1 найдутся  такие, что
такие, что  , что противоречит условию. ■
, что противоречит условию. ■
Пример. Доказать, что:
а) векторы 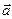 и
и  линейно зависимы тогда и только тогда, когда они коллинеарные;
линейно зависимы тогда и только тогда, когда они коллинеарные;
б) векторы 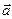 ,
,  ,
,  линейно зависимы тогда и только тогда, когда они компланарны.
линейно зависимы тогда и только тогда, когда они компланарны.
Доказательство:
а) Пусть 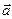

 . Если
. Если  , то
, то  и коллинеарность
и коллинеарность  и
и  влечет линейную зависимость
влечет линейную зависимость  и
и  .
.
Если  и
и  коллинеарные, то согласно признаку коллинеарности, существует такое
коллинеарные, то согласно признаку коллинеарности, существует такое  , что
, что  , т.е.
, т.е.  ,
,  , и линейная зависимость
, и линейная зависимость 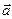 и
и  очевидна.
очевидна.
б) Пусть 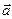 ,
,  и
и  компланарны. Если векторы
компланарны. Если векторы 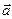 и
и  коллинеарные, то из доказанного следует
коллинеарные, то из доказанного следует  при некоторых
при некоторых  и
и  таких, что
таких, что  . Но тогда
. Но тогда  , причем
, причем  , т.е.
, т.е. 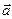 ,
,  ,
,  линейно зависимы.
линейно зависимы.
Пусть теперь компланарные векторы 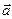 ,
,  ,
,  таковы, что
таковы, что 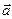 и
и  не коллинеарные. Тогда вектор
не коллинеарные. Тогда вектор  можно разложить по базису
можно разложить по базису  :
:  . Отсюда
. Отсюда  , причём
, причём  , т.е.
, т.е. 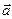 ,
,  ,
,  линейно зависимы.
линейно зависимы.
п. 5 Линейные операции над векторами
в координатной форме
Пусть  – некоторая аффинная система координат в пространстве.
– некоторая аффинная система координат в пространстве.
Теорема 1. Пусть векторы  и
и  . Тогда:
. Тогда:
1.  ;
;
2. 
Доказательство:
1. Рассмотрим векторы 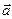 и
и  :
:  ,
,  . Тогда сумма векторов
. Тогда сумма векторов 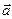 и
и  :
: 


 .
.
2. 
 . ■
. ■