IV Выражение векторного произведения через проекции

Приведем таблицу векторного умножения базисных векторов , легко получаемую из рисунка

 

 

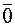
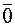
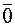
В столбце базисных векторов приведены первые множители векторного произведения, а в строке – вторые.

Пусть известны проекции векторов и в некоторой ДПСК: , . Разложим векторы по базису

и векторно перемножим эти “многочлены” почленно. Учитывая приведенную таблицу, получим:

 

В этой формуле нетрудно заметить формальное разложение некоторого определителя третьего порядка по элементам, например, первой строки. Итак, имеем

Пример. Найти площадь ΔАВС, где А(1;1;1), B(2;2;2) и C(4;3;5).

Решение. Найдем векторы и . Перемножим их векторно:

Модуль этого вектора – это площадь параллелограмма, построенного на 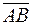и , а половина этого модуля – искомая площадь треугольника:

Вектор обладает важным свойством, которое понадобится нам в дальнейшем: этот вектор перпендикулярен векторам 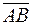и или, другими словами, этот вектор перпендикулярен плоскости ΔАВС.