II. Примеры использования функций
Пример 1. Игральная кость подбрасывается 24 раза. Найти вероятность того, что 6 очков выпадут ровно 3 раза. Найти точное значение вероятности и приближенные, используя локальную формулу Муавра-Лапласа и формулу Пуассона.
Решение.Требуется найти вероятность того, что в n=24 испытаниях по схеме Бернулли с вероятностью успеха 1/6, число успехов будет равно 3. Для точного вычисления вероятности используем функцию БИНОМРАСП.Если параметринтегральная имеет значение ЛОЖЬ (0), то функция БИНОМРАСП возвращает вероятность того, что число успешных испытаний в точности равно значению аргумента число успехов. Таким образом, для  ,
,  ,
,  находим:
находим:
 =БИНОМРАСП(3;24;1/6;0)=0,203681.
=БИНОМРАСП(3;24;1/6;0)=0,203681.
Найдем приближенное значение вероятности, используя локальную формулу Муавра-Лапласа. Согласно этой формуле, вероятность  , т.е. приближенно равна плотности нормального распределения со средним
, т.е. приближенно равна плотности нормального распределения со средним  и среднеквадратичным отклонением
и среднеквадратичным отклонением 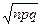 в точке
в точке  . Значения плотности распределения нормальной величины возвращает функция НОРМРАСП, при значении параметраинтегральная равном ЛОЖЬ (0).
. Значения плотности распределения нормальной величины возвращает функция НОРМРАСП, при значении параметраинтегральная равном ЛОЖЬ (0).
Таким образом: 
 НОРМРАСП(
НОРМРАСП(  )=0,188073.
)=0,188073.
Найдем приближенное значение той же вероятности, используя формулу Пуассона. Согласно этой формуле, при малых 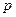 вероятность
вероятность  , т.е. приближенно равна вероятности пуассоновского распределения с параметром (средним значением)
, т.е. приближенно равна вероятности пуассоновского распределения с параметром (средним значением)  в точке
в точке  . Вероятности отдельных значений для распределения Пуассона возвращает функция ПУАССОН при значении параметраинтегральная равном ЛОЖЬ (0). Таким образом:
. Вероятности отдельных значений для распределения Пуассона возвращает функция ПУАССОН при значении параметраинтегральная равном ЛОЖЬ (0). Таким образом: 
 ПУАССОН(
ПУАССОН( 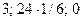 )=0,195367.
)=0,195367.
Заметим, что погрешность при использовании формулы Муавра-Лапласа составила  7,8%, а при использовании формулы Пуассона
7,8%, а при использовании формулы Пуассона  4,1%.
4,1%.
Пример 2. Вероятность искажения одного символа при передачи сообщения равна 0,01. Какова вероятность, что сообщение, содержащее 200 символов, содержит не более 2-х искажений. Найти точное значение вероятности и приближенные, используя локальную формулу Муавра-Лапласа и формулу Пуассона.
Решение.Требуется найти вероятность того, что в n=200 испытаниях по схеме Бернулли с вероятностью успеха 0,01, число успехов будет не более 2. Для точного вычисления вероятности используем функцию БИНОМРАСП.Если параметринтегральная имеет значение ИСТИНА (1), то функция БИНОМРАСП возвращает вероятность того, что число успешных испытаний лежит в пределах от 0 до значения, определяемого аргументом число успехов. Таким образом, для  ,
,  ,
, 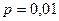 находим:
находим:  =БИНОМРАСП(2;200;0,01;1)=0,676679.
=БИНОМРАСП(2;200;0,01;1)=0,676679.
Найдем приближенное значение вероятности, используя локальную формулу Муавра-Лапласа. Согласно этой формуле, вероятность  , приближенно равна плотности нормального распределения в точке
, приближенно равна плотности нормального распределения в точке  со средним
со средним  и среднеквадратичным отклонением
и среднеквадратичным отклонением 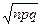 . Значения плотности распределения нормальной величины возвращает функция НОРМРАСП, при значении параметраинтегральная равном ЛОЖЬ (0). Таким образом:
. Значения плотности распределения нормальной величины возвращает функция НОРМРАСП, при значении параметраинтегральная равном ЛОЖЬ (0). Таким образом: 

 НОРМРАСП(
НОРМРАСП(  )+НОРМРАСП(
)+НОРМРАСП(  )+НОРМРАСП(
)+НОРМРАСП(  )=0,607013.
)=0,607013.
Найдем приближенное значение той же вероятности, используя формулу Пуассона. Согласно этой формуле, вероятность  при малых
при малых 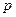 приближенно равна вероятности пуассоновского распределения в точке
приближенно равна вероятности пуассоновского распределения в точке  со средним значением
со средним значением  . Значения вероятностей для распределения Пуассона возвращает функция ПУАССОН. Причем, если значение параметраинтегральная равно ИСТИНА (1), то функция ПУАССОН возвращает вероятность того, что случайная величина, имеющая распределение Пуассона примет значения в пределах от 0 до значения, определяемого аргументом x. Таким образом:
. Значения вероятностей для распределения Пуассона возвращает функция ПУАССОН. Причем, если значение параметраинтегральная равно ИСТИНА (1), то функция ПУАССОН возвращает вероятность того, что случайная величина, имеющая распределение Пуассона примет значения в пределах от 0 до значения, определяемого аргументом x. Таким образом: 
 ПУАССОН(
ПУАССОН(  )=0,676676.
)=0,676676.
Заметим, что погрешность, полученная при использования формулы Пуассона, в данном случае на порядок ниже, чем при использовании локальной формулы Муавра-Лапласа. Смысла использовать интегральную формулу Муавра-Лапласа в данном случае нет, поскольку интервал значений  мал
мал  .
.
Найдем приближенное значение вероятности, используя теперь интегральную формулу Муавра-Лапласа. Согласно этой формуле, вероятность  , т.е. приближенно равна вероятности попадания в интервал
, т.е. приближенно равна вероятности попадания в интервал 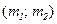 нормальной случайной величины со средним
нормальной случайной величины со средним  и среднеквадратичным отклонением
и среднеквадратичным отклонением 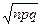 . Следовательно, если
. Следовательно, если  - функция распределения нормальной случайной величины с параметрами
- функция распределения нормальной случайной величины с параметрами  и
и  , то
, то 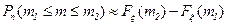 . Значения функции распределения нормальной величины возвращает функция НОРМРАСП, при значении параметраинтегральная равном ИСТИНА (1). Таким образом:
. Значения функции распределения нормальной величины возвращает функция НОРМРАСП, при значении параметраинтегральная равном ИСТИНА (1). Таким образом:  НОРМРАСП(
НОРМРАСП(  -НОРМРАСП(
-НОРМРАСП(  =.
=.
Пример 3. Монета подбрасывается 10000 раз. Найти вероятность того, что орел выпадет более 5100 раз. Найти точное значение вероятности и приближенное, используя интегральную формулу Муавра-Лапласа.
Решение.Требуется найти вероятность того, что в n=10000 испытаниях по схеме Бернулли с вероятностью успеха 1/2, число успехов будет более 5100. Для точного вычисления вероятности используем функцию БИНОМРАСП.Если параметринтегральная имеет значение ИСТИНА (1), то функция БИНОМРАСП возвращает вероятность того, что число успешных испытаний не менее значения аргумента число успехов. Таким образом, находим:  1-БИНОМРАСП(5100;10000;1/2;1)=0,022213.
1-БИНОМРАСП(5100;10000;1/2;1)=0,022213.
Найдем приближенное значение вероятности, используя интегральную формулу Муавра-Лапласа. Согласно этой формуле, вероятность  , т.е. приближенно равна вероятности попадания в интервал
, т.е. приближенно равна вероятности попадания в интервал 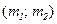 нормальной случайной величины со средним
нормальной случайной величины со средним  и среднеквадратичным отклонением
и среднеквадратичным отклонением 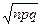 . Следовательно, если
. Следовательно, если  - функция распределения нормальной случайной величины с параметрами
- функция распределения нормальной случайной величины с параметрами  и
и  , то
, то 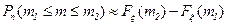 .
.
Значения функции распределения нормальной величины возвращает функция НОРМРАСП, при значении параметраинтегральная равном ИСТИНА (1). Таким образом:
 НОРМРАСП(
НОРМРАСП( 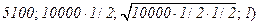 )=0,02275.
)=0,02275.
Заметим, что более точной является приближенная формула  . Если использовать ее, то получим:
. Если использовать ее, то получим:

=НОРМРАСП( 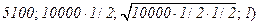 )=0,022216.
)=0,022216.
Пример 4. Случайная величина распределена по нормальному закону с параметрами  и
и  . Найти:
. Найти:
а) вероятность того, что  примет значение в интервале
примет значение в интервале  ;
;
б) квантиль распределения уровня  5;
5;
в) критическую точку распределения уровня 0,07;
г) интервал, симметричный относительно математического ожидания, в котором с вероятностью 0,95 содержатся значения  .
.