И совокупного показателя взаимосвязи
Исчисление показателей связи величин дополняет показатели их независимости. Последние введены Келле ещё в 1919 г. и названы показателями алиенации. Так парному показателю связи rAB соответствует парный показатель независимости ŕAB = 
.
Совокупный показатель независимости, например, А от В и С, определяется формулой ŔA.BC = 
,где RA.BC– совокупный коэффициент корреляции. В [7] доказана следующая Лемма:
Коррелируя стохастическую величину А с остатком, полученным после очистки А от влияния В и С, получим ŔA.BC.
Согласно леммы показатель независимости ŔA.BCможетбыть получен, например, по такой укрупнённой схеме:
1. Очистить В от С;
2. Очистить А от С;
3. Очистить второй остаток от первого;
4. Коррелируя третий остаток с А, получаем ŔA.BC.
Необходимые при этом построения отражены на Рис. 5. Ключевое содержание этим построениям придаёт задача сопоставимости.
Покажем, что 
перпендикулярен к плоскости [cOb]. ┴ 
по построению и 
┴ 
┴ 
. Отсюда ┴ , что и требовалось показать. ∆Oda – прямоугольный с прямым углом при вершине d. ŔA.BC = ║ 
║ / ║ 
║ = cos ψ.
Найдём формулу выражения для cos ψ. Очевидно, что aO = ad / cos ψ, аca = ad / sin φ и aO = aca / sin β = ad / sin β * sin φ. Отсюда cos ψ = sin β * sin φ или ŔA.BC = * 
, что соответствует (5) – (6).
На основании проделанного построения предлагается следующая схема исчисления совокупного алиенационного отношения (в своём начале она полностью повторяет ранее изложенную схему частного корреляционного отношения).
Таблица 5
Схема исчисления частного корреляционного отношения
| № п/п | Логические операции | Содержание операции для случая линейной регрессии |
Коррелирование остатков  и 
| rAB.C = (  ,  )
| |
| Очистка от
|  = - * rAB.C
| |
Исчисление единицы масштаба 
| S( ) = 1 / (║ ║ * ) =
1 / *
| |
| Сопоставление и
| Ok0 = * S( ),  = * SA
| |
| Стабилизация
| Аналогично операции стабилизации в схеме 1 | |
| Коррелирование остатков и Oa0
| ŔA.BC = ( , )
|
Предложение 5: При линейной форме связи группы случайных величин их совокупное корреляционное отношение совпадает с совокупным коэффициентом корреляции.
До сих пор рассматривались логические структуры известных статистике показателей. В качестве демонстрации возможностей понимания аспекта сопоставимости, рассмотрим структуру совокупного показателя взаимосвязи, соответствующего RA.BC. Из Рис. 5 видно, что, коррелируя с , сразу получим RA.BC (это следует из cos(π / 2 – ψ) = sin ψ.Угол <aOdобозначим ξ.Очевидно, что ξ + ψ = π / 2, sin ψ = RA.BC = cos ξ, = - ŔA.BC * S( ) * . (9)
По (9) легко построить схему исчисления совокупного показателя взаимосвязи. Необходимые при этом построения отображены на Рис. 6. В начальной своей части схема совокупного показателя взаимосвязи полностью совпадает со схемой частного показателя взаимосвязи.
Таблица 6
Схема исчисления совокупного показателя взаимосвязи
| № п/п | Логические операции | Содержание операции для случая линейной регрессии |
| Очистка от
| =  * rAB.C * 
| |
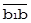
| Исчисление единицы масштаба
| S( ) = 1 / (║ ║ * * )
| |
| Представление в масштабе А
| S = S( ) / S( ) = 1 / *
| |
| Проецирование на
| b  A.dc = ŔA.BC * S = 1(10)
| |
| Очистка от
| = - b A.dc *
| |
| Исчисление единицы масштаба
| S( )= 1 / (║ ║ *  )
| |
| Представление в масштабе
| S = 1 /
| |
| Проецирование на . Получение совокупного показателя взаимосвязи
| ║  ║ = RA.BC * S * ║ ║,
bA.BC = RA.BC * S = 1(11)
|
Интересна интерпретация результатов (10) – (11). Так как bA.BC = 1,это означает, что теоретическая часть рассеяния результативного фактора А, объяснённая линейной регрессией с В и С, совпадает с .