Упражнение

1.1. Доказать:

а) два вектора линейно зависимы тогда и только тогда, когда они коллинеарны;

б) доказать, что три вектора линейно зависимы тогда и только тогда, когда они компланарны;

в) любые четыре вектора линейно зависимы.

1.2. Докажите, что вектора 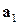, , 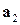…, 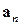линейно независимы тогда и только тогда, когда равенство 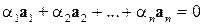выполняется лишь при нулевых коэффициентах , , …, .

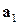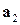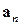1.3. Доказать, что радиус-вектор центра правильного многоугольника есть среднее арифметическое радиус-векторов его вершин.

1.4. В точках пространства, имеющих радиус-векторы , сосредоточены массы . Найти радиус-вектор центра тяжести этой материальной системы.

1.5. Доказать, что если диагонали четырехугольника в точке пересечения делятся пополам, то этот четырехугольник – параллелограмм.

1.6. Доказать, что средняя линия трапеции параллельна основаниям, а длина средней линии равна полусумме длин оснований (теорема о средней линии трапеции).

1.7. Какому условию должны удовлетворять три вектора, чтобы из них можно было образовать треугольник?

1.8. Можно ли построить треугольник, стороны которого равны и параллельны медианам данного треугольника?

1.9. Пусть векторы некомпланарны. Показать, что четыре точки и ,где , лежат в одной плоскости тогда и только тогда, когда

1.10. Даны радиус-векторы вершин треугольника. Доказать, что медианы треугольника пересекаются в одной точке, и найти радиус-вектор этой точки.

1.11. Доказать, что биссектрисы треугольника пересекаются в одной точке.

1.12. Даны радиус-векторы вершин треугольника и длины его сторон. Найти радиус-вектор точки пересечения биссектрис треугольника.

 

 

Вопросы для самопроверки

1. Почему повороты не являются векторными величинами?

2. Что такое аксиальный вектор?

3. Сформулируйте различные критерии линейной (не)зависимости.

4. Какова связь коллинеарности и компланарности с линейной зависимостью?