Векторное произведение двух векторов, заданных своими проекциями.
Пусть даны векторы  и
и  , тогда
, тогда
 .
.
Если разложить определитель по элементам первой строки, то
 =
=  .
.
Механический смысл векторного произведения.
Пусть в точке 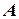 к диску приложена сила
к диску приложена сила  . Определить момент силы
. Определить момент силы  относительно точки
относительно точки 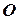 на диске.
на диске.
 Пусть
Пусть  - радиус-вектор точки приложения силы
- радиус-вектор точки приложения силы  ,
,  - плечо, т.е. расстояние от точки
- плечо, т.е. расстояние от точки  до вектора силы
до вектора силы  ,
,  - угол между векторами
- угол между векторами  и
и  ,
, 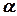 - плоскость диска. Векторы
- плоскость диска. Векторы  и
и  принадлежат диску (
принадлежат диску (  ).
).

Отсюда следует, что  .
.
Пример 11. Сила  приложена в точке
приложена в точке  . Определить момент силы относительно точки
. Определить момент силы относительно точки  .
.
Решение. Образуем вектор  . Тогда момент относительно точки
. Тогда момент относительно точки  вычисляется по формуле:
вычисляется по формуле:  . Отсюда
. Отсюда
 , или
, или  .
.