Верное доказательство.
Введём функцию f(x) = 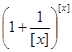 (x ³ 1).
(x ³ 1).
При n £ x < n + 1: f(x) = 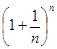 , поэтому
, поэтому 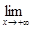 f(x) = e.
f(x) = e.
Воспользуемся неравенствами: [x] £ x < [x +1] = [x] + 1. Отсюда при x ³ 1 имеем:
 <
< 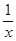 £
£ 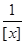 а, следовательно, 1 +
а, следовательно, 1 +  < 1+
< 1+ 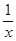 £ 1 +
£ 1 + 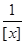 .
.
Поэтому
 £
£ 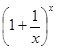 £
£ 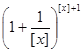 или
или
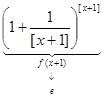
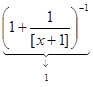
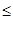
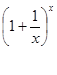
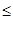

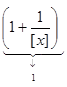 .
.
Отсюда следует, что 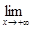
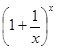 = е.
= е.
Положим у = 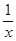 . Тогда y ® +0, если х ® +¥ и мы получаем,
. Тогда y ® +0, если х ® +¥ и мы получаем,
что 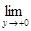 (1 + у)1/у = е или
(1 + у)1/у = е или
 (1 + х)1/х = е. (1)
(1 + х)1/х = е. (1)
Рассмотрим теперь 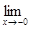 (1 + х)1/х. Положим у = - х. Тогда y ® +0, если х ® -0.
(1 + х)1/х. Положим у = - х. Тогда y ® +0, если х ® -0.
(1 + х)1/х = (1 - у)-1/у=  =
=  .
.
Положим  = z. Тогда z ® +0, если y ® +0 и y =
= z. Тогда z ® +0, если y ® +0 и y =  ,
,  =
=  +1.
+1.
Таким образом, (1 + х)1/х=  =(1 + z)1/z+1. Если х ® -0, то z ® +0, поэтому
=(1 + z)1/z+1. Если х ® -0, то z ® +0, поэтому
(1 + z)1/z+1= 
 ® e.
® e.
Итак, 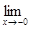 (1 + х)1/х = е. (2)
(1 + х)1/х = е. (2)
Из (1) и (2) следует, что 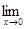 (1 + х)1/х = е.
(1 + х)1/х = е.