Скалярное произведение двух векторов
План ответа
1. Скалярное произведение двух векторов. Определение, свойства, координатная форма.
2. Векторное произведение векторов. Определение, свойства, геометрический смысл, координатная форма.
3. Смешанное произведение трех векторов. Определение, свойства, геометрический смысл, координатная форма.
4. Приложение скалярного, векторного, смешанного произведения векторов к решению задач. Вычисление площадей и объемов фигур, нахождение расстояний от точки до прямой в трехмерном пространстве, между скрещивающимися прямыми и т.д.
Скалярное произведение двух векторов
 Пусть имеются два ненулевых вектора
Пусть имеются два ненулевых вектора 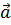 и
и 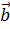 . Построим их представителей
. Построим их представителей 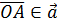 и
и 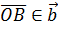 с началом в точке О. Проведём лучи OA и OB.
с началом в точке О. Проведём лучи OA и OB.
Определение. Углом между векторами 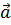 и
и 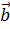 называется угол
называется угол  .
.
Обозначение: 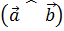 .
.
Замечание. Угол между векторами не зависит от выбора точки O.
Если 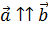 , то
, то 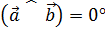 ; если
; если  , то
, то 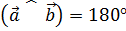 .
.
Определение. Два ненулевых вектора 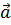 и
и 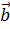 называются перпендикулярными, если
называются перпендикулярными, если 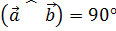 .
.
Обозначение: 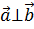 .
.
Таким образом, для любых векторов 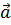 и
и 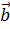 справедливо:
справедливо: 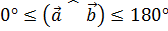 .
.
Определение. Скалярным произведением двух векторов 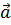 и
и 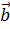 называется число, равное произведению длин этих векторов на косинус угла между ними.
называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначение:  .
.
Простейшие свойства скалярного умножения
1. Критерий перпендикулярности двух векторов: 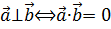 .
.
2. 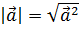 , где
, где 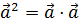 – скалярный квадрат вектора
– скалярный квадрат вектора 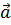 .
.
Теорема. Пусть в базисе 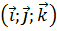 векторы имеют координаты:
векторы имеют координаты: 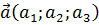 ,
, 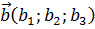 . Тогда ng w:val="EN-US" w:fareast="RU"/></w:rPr><m:t>b</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:fareast="RU"/></w:rPr><m:t>3</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
. Тогда ng w:val="EN-US" w:fareast="RU"/></w:rPr><m:t>b</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:fareast="RU"/></w:rPr><m:t>3</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 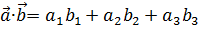 .
.
Следствие 1. Пусть 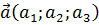 ,
, 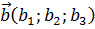 в базисе
в базисе 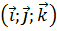 . Тогда:
. Тогда:
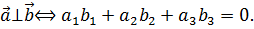
Следствие 2. Пусть 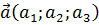 ,
, 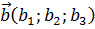 два ненулевых вектора в ортонормированном базисе
два ненулевых вектора в ортонормированном базисе 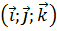 . Тогда:
. Тогда:
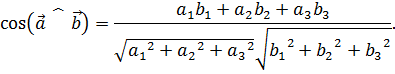
Алгебраические свойства скалярного умножения
Теорема. Для любого 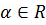 и для любых векторов
и для любых векторов  справедливы равенства:
справедливы равенства:
1. 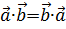 ;
;
2. 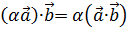 и
и 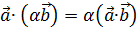 ;
;
3. 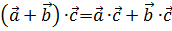 .
.
Следствие. Для любых векторов 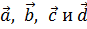 справедливо:
справедливо: