Введение

ОСНОВЫ ТЕОРИИ УПРАВЛЕНИЯ

Тема 3. СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Моя временная функция неожиданно оступилась и рухнула в трещину, а частотная функция рванула на бесконечность в нецензурном формате. На этой же математике преобразования меня и вытаскивали. Чем ближе к поверхности, тем литературней формат. Надо бы заняться теорией кризисных ситуаций.

Валерий Самойлин. Геофизик, радиоинженер, альпинист. ХХ в.

Единственный способ противостоять природе, основательно познать ее.

Джон Локк. 1693 г.

Содержание

Введение.

1. Структура и функциональные компоненты САУ. Основные компоненты САУ. Укрупненная схема системы управления. Управление сложными системами. Локальные задачи управления. Многоканальное управление. Регуляторы и задающие блоки. Специальные блоки систем управления.

2. Математическая модель объекта управления. Система линейных уравнений объекта. Передаточная функция системы. Типовые звенья САУ. Типовые входные воздействия.

3. Временные характеристики САУ. Понятие временных характеристик. Экспериментальное определение временных параметров. Физическая реализуемость.

4. Частотные характеристики САУ. Понятие частотных характеристик. Годограф. Логарифмические частотные характеристики.

5. Характеристики элементарных звеньев систем. Безинерционное (пропорциональное, усилительное) звено, Апериодическое инерционное звено первого порядка. Интегрирующее (астатическое) звено. Интегрирующее звено с замедлением. Идеальное дифференцирующее звено. Дифференцирующее звено с замедлением. Апериодическое звено второго порядка. Колебательное звено.

6. Построение моделей вход-выход. Простейшие соединения блоков. Передаточные функции систем управления.

Введение

Управление объектом с помощью технических средств без участия человека называется автоматическим управлением. Теория автоматического управления (ТАУ) это наука, которая изучает процессы управления и проектирования систем автоматического управления, работающих по замкнутому циклу с обратной связью. Совокупность объекта управления и средств автоматического управления называется системой автоматического управления (САУ). Основной задачей автоматического управления является поддержание определенного закона изменения одной или нескольких физических величин в объекте управления.

Основные задачи теории автоматического управления:

• анализ устойчивости, свойств, динамических показателей качества и точности САУ;

• синтез алгоритмов (аналитических выражений), описывающих САУ и обеспечивающих оптимальное качество управления;

• моделирование САУ с использованием компьютеров и универсальных либо специализированных (предметно-ориентированных) прикладных программ;

• проектирование САУ с использованием аппаратных средств вычислительной техники и их программного обеспечения (средств автоматизации программирования и проч.).

Отметим, что проектирование, внедрение и эксплуатация современных САУ подразумевает тесное взаимодействие специалистов различных профилей, и, в первую очередь, технологов, знающих «физические» особенности управляемых процессов; специалистов по автоматическому управлению, обеспечивающих разработку САУ (алгоритмов управления и контроля), и специалистов по средствам автоматизации программирования.

3.1. СТРУКТУРА И ФУНКЦИОНАЛЬНЫЕ КОМПОНЕНТЫ САУ [1].

Основные компоненты САУ. Система автоматического управления содержит следующие компоненты, обеспечивающие ее функционирование (рис. 3.1.1): объект управления ОУ (управляемый процесс); исполнительные устройства ИсУ; измерительные устройства ИзУ; устройство управления УУ.

Объектами управления технических систем служат кинематические механизмы, электрические системы, тепловые, химические и другие технологические процессы. Состояние объекта характеризуется переменными состояния, к которым относятся угловые и линейные координаты, скорости и другие механические переменные, описывающие движения кинематических механизмов; токи или напряжения электрических элементов схемы; температуры и плотности веществ в тепловых и химических процессах, и любые другие физические величины. Переменные состояния объединяются в вектор состояния.

Рис. 3.1.1.

К регулируемым, или выходным, переменным y_j = y_j(t) относятся переменные ОУ, по отношению к которым формулируется основная задача управления. Выходные переменные объединяются в вектор выхода. Для кинематических механизмов вектор выхода обычно представлен декартовыми координатами рабочей точки механизма.

Входами ОУ являются управляющие органы, к которым прикладываются воздействия U_j исполнительных устройств ИсУ системы. Это входные оси кинематических механизмов, входные схемы электрических систем, нагревательные элементы и вентили тепловых и химических процессов, к которым приложены силы или моменты сил электроприводов, электрические напряжения и т. д., вызывающие движение (развитие) управляемого процесса.

Объекты с одним входом и одним выходом называются одноканальными. К многоканальным относят объекты с несколькими входами и/или выходами. Они могут иметь каналы, независимые или взаимозависимые друг от друга (многосвязные объекты).

К внешней среде системы управления относятся процессы, оказывающие влияние на поведение управляемого объекта. Среда является источником помех измерения d_j(t), возмущающих воздействий f_j(t), внешних задающих воздействий.

К возмущающим относят воздействия, препятствующие функционированию объекта. Это могут быть силы сопротивления или трения для кинематических механизмов, температура окружающей среды для тепловых процессов и т. д. Возмущающие воздействия объединяются в вектор возмущений.

Измерительные устройства ИзУ (датчики) предназначены для получения информации об объекте и внешней среде (сигналов y'_j), т. е. для электрического измерения выходных переменных, переменных состояния и внешних задающих воздействий. Различают следующие типы измерительных устройств:

• датчики внутренней информации, предназначенные для измерения переменных объекта (системы управления);

• датчики внешней информации (сенсоры, средства внешнего контроля) - измерители состояния внешней среды либо положения объекта по отношению к внешним объектам.

В состав измерительных устройств часто включают также вычислительные блоки, осуществляющие первичную обработку информации.

Исполнительные устройства ИсУ - это устройства, предназначенные для усиления маломощных управляющих сигналов u_j и создания энергетических воздействий U_j на входах объекта, т. е. управляемые источники механической, электрической или тепловой энергии (электропривод, преобразователь электрической энергии в механическую, и т.п.).

Устройство управления УУ - это блок, обрабатывающий полученную с помощью измерителей текущую информацию о состоянии объекта и внешней среды и формирующий управляющие воздействия u_j (информационные сигналы), поступающие на исполнительные устройства объекта. В функции устройства управления входит:

• идентификация объекта и среды (анализ их текущего состояния и параметров);

• генерация внутренних задающих воздействий;

• расчет управляющих воздействий u_j по предписанным формулам (алгоритмам).

Укрупненная схема системы управления может быть представлена в виде двух основных блоков, взаимодействующих с внешней средой (рис. 3.1.2).

Объект управления (ОУ) - комплекс элементов системы, включающий в свой состав собственно объект, измерительные и исполнительные устройства. Эта часть САУ обычно проектируется и комплектуется как единое целое и является ее неизменяемой частью. Динамические свойства ОУ (математическая модель) находятся с использованием известных физических законов.

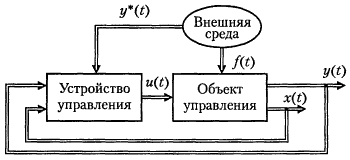Рис. 3.1.2.

Устройство управления (УУ) - блок, выполняющий вычислительные функции, слабо связанные с физической природой ОУ. Алгоритм его работы определяется динамическими свойствами управляемого процесса (математической моделью ОУ) и задачами системы управления. Современные УУ представляют собой универсальные или специализированные средства вычислительной техники. Их программное обеспечение составляют системные средства и специальные прикладные программы, осуществляющие расчет управляющих воздействий u(t).

Управление сложными системами. Сложная система имеет в своем составе большое число взаимодействующих подсистем и обеспечивает решение сложных комплексных задач. К таким системам относятся информационные сети (телефонные, локальные, Интернет), транспортные сети, производственные процессы, системы управления динамическими объектами (воздушными, космическими), и т.п.

Сложные системы управления имеют следующие признаки:

• комплексный характер управляемого процесса (объекта), наличие нескольких взаимосвязанных локальных объектов управления;

• необходимость последовательного решения задачи управления, поочередного выполнения основных действий системы или локальных объектов;

• иерархическая структура задач управления.

Основным в понятиях сложной задачи и сложной системы является их структурируемость, т. е. возможность разбиения на компоненты меньшей сложности. Выбор таких компонент неоднозначен, а используемая при этом терминология достаточно условна. Принято выделять задачи управления стратегического, тактического и локального уровня.

К стратегическим задачам относят задачи общего технологического характера, поддержания определенной последовательности действий сложного комплексного процесса: изготовление продукта, управление полетом и проч.

Тактическая задача - элемент общей стратегической задачи, устанавливающий требования к поведению каждого элементарного объекта сложной системы и/или осуществлению элементарного режима. К тактическим задачам управления относится задача управления обработкой детали на станке, управления циклом химического процесса.

Локальная задача - это задача изменения или поддержания состояния элементарного объекта. К локальным относятся, в частности, задачи стабилизации скорости вращения двигателя, слежение за внешним объектом или задающим сигналом, и т.п.

Рис. 3.1.3.

Таким образом, понятие сложной задачи предусматривает возможность расчленения общей стратегической задачи на ряд более простых задач, решаемых последовательно или параллельно. Отсюда вытекают следующие принципы управления сложной системой:

• декомпозиция - расщепление сложной задачи и сложного объекта на более простые компоненты (подзадачи и локальные объекты);

• децентрализация - выделение собственных устройств управления или программных средств (алгоритмов), обеспечивающих решение отдельных подзадач управления локальными объектами;

• иерархическое управление - введение определенной подчиненности подзадач разного уровня сложности и соответствующей подчиненности устройств управления;

• многорежимное управление (временная декомпозиция) - последовательное переключение решаемых задач и устройств управления.

Локальные задачи управления устанавливают желаемый характер изменения переменных объекта управления. В зависимости от структуры объекта различают задачи одноканального и многоканального управления (рис. 3.1.3).

В одноканальных задачах управления, к которым относятся задачи стабилизации, слежения и терминального управления, выходная переменная y(t) является скалярной функцией времени.

Рис. 3.1.4.

Задача стабилизации или регулирования (рис. 3.1.4-а) формулируется как задача поддержания выходной переменной на заданном уровне у_зад = у* = const:

y(t) → у* = const, t → ∞.

Задача слежения (рис. 3.1.4-b) - это задача соблюдения заданного закона y*(t) изменения переменной у(t):

y(t) → у*(t), t → ∞.

При этом различают:

• задачи слежения за внешним объектом, когда функция y*(t) является выходом внешнего объекта и заранее неизвестна;

• задачи программного управления, в которых программа движения y*(t) генерируется специальным задающим блоком ЗБ, входящим в состав САУ.

Система автоматического управления, решающая задачу слежения, называется следящей системой. Сигнал y*(t), определяющий требуемый закон движения системы, называется задающим воздействием. Сигнал

e(t) = y*(t) – y(t),

характеризующий текущее значение отклонения выходной переменной от задающего воздействия, называется рассогласованием, отклонением или ошибкой управления. Задачи стабилизации и слежения иначе могут быть сформулированы как задачи поддержания нулевого значения рассогласования, т. е. e(t) → 0.

Задача терминального управления заключается в "перемещении" объекта управления в заданную конечную (терминальную) точку y_f:

y → y_f = const.

Особенность терминальной задачи, в отличие от стабилизации, заключается в том, что величина начального отклонения e(0) = y_f – у(0) может быть достаточно велика. Это обусловливает необходимость выбора особой стратегии управления (минимизации быстродействия или энергетических затрат, ограничений на управляющие сигналы и переменные состояния и т.д.).

Полное устранение рассогласования e в реальных системах не достигается, в силу влияния на систему в реальной среде возмущающих воздействий f(t), ограниченной точности измерительных датчиков и погрешности работы собственно системы стабилизации. Для оценки эффективности решения задач управления вводятся показатели качества управления.

Различают динамические показатели, определяющие качество переходного режима работы системы, к которым относятся различные количественные (числовые) оценки быстродействия и колебательности системы, и точностные показатели, определяющие погрешность системы в установившемся режиме, т. е. по окончании переходного процесса. К динамическим показателям относятся время переходного процесса t_o (от момента воздействия на систему управляющего или возмущающего сигнала до момента установления нового стабильного состояния равновесия с заданной степенью погрешности) и перерегулирование (относительная величина первого, как правило – максимального, выброса ошибки e(t) на колебательном переходном процессе), а к точностным — погрешность стабилизации или слежения, которая связана с установившимся значением ошибки e_у(t) при t→ ∞ в номинальном равновесном состоянии системы.

Многоканальное управление. В многоканальных задачах управления выходом объекта служит векторная переменная (вектор выхода), и, следовательно, векторными переменными являются также задающие воздействия (вектор задания) и рассогласование (вектор ошибок). Формулировки основных задач многоканального управления (стабилизации, слежения и терминального управления) практически не отличаются от одноканальных. Кроме них для многоканальных объектов возникают задачи декомпозиции и согласованного управления.

Задача согласованного управления предусматривает организацию принудительного взаимодействия каналов системы с целью поддержания заданных соотношений выходных переменных y_j(t). Такие соотношения (условия согласования), в простейших случаях принимают вид равенств вида у₁(t) = f(y₂(t)), соответствующих синхронному движению отдельных частей (каналов) сложной системы. В более общем случае условия согласования записываются в виде: f(y₁, y₂) =0, где f(•) - заданная функция. Согласованное управление требует координации управляющих воздействий u_j(t).

Наиболее наглядные задачи терминального и согласованного управления возникают при управлении пространственным движением многозвенных механических объектов (роботов, станочных механизмов, транспортных средств). Здесь в качестве выходных переменных системы обычно выступают декартовы координаты y_j рабочей точки механизма в трехмерном физическом пространстве R³ или двумерном R² , а задача перемещения рабочей точки механизма из начального положения в точку {y_fj} относится к многоканальным терминальным задачам.

Задача декомпозиции в противоположность задаче согласования заключается в устранении взаимного влияния каналов системы с целью сведения задачи управления многосвязным объектом к нескольким более простым одноканальным задачам. Это достигается с помощью соответствующих алгоритмов коррекции управляющих воздействий.

Регуляторыи задающие блоки. В состав устройства управления системы, предназначенной для решения локальных задач, входят задающий блок (ЗБ) и регулятор выходных переменных (рис. 3.1.5).

Рис. 3.1.5.

В современных системах блоку не обязательно соответствует физическое устройство. Это может быть и алгоритм или программа расчетов требуемых переменных (сигналов).

Регулятором называется блок (алгоритм), рассчитывающий управляющее воздействие u(t) с целью решения локальной задачи управления. Регуляторы в системах автоматизации служат для обеспечения определенного качества стабилизации технологических параметров на заданном уровне. Алгоритмом управления называется набор аналитических выражений, используемых для расчета управляющих воздействий, или система операций, выполняемых по определенным правилам. Типовой алгоритм управления, это математическая зависимость между выходным регулирующим воздействием u(t) и входным отклонением ε регулируемой величины y от заданного значения y*. Входной величиной для регулятора является сигнал ε, а выходной – регулирующее воздействие u:

u(t) = U(e(t),у*(t),...).

В качестве оператора U(•) могут выступать как алгебраические и трансцендентные функции, так и интегро-дифференциальные операторы, булевы функции и пр.

Простейшими алгоритмами управления (регуляторами) являются регуляторы отклонения вида: u(t) = U(e(t)). В практике принято рассматривать три типовых закона регулирования: пропорциональный П, интегрирующий И, дифференцирующий Д. На базе этих законов в регуляторах реализуют более сложные алгоритмы, являющиеся комбинацией основных: пропорционально-интегральный ПИ, пропорционально-дифференциальный ПД, пропорционально-интегрально- дифференциальный ПИД, и т.п.

Уравнения основных типовых регуляторов:

• П - пропорциональный (статический):

u(t) = k_пe(t), W(p) = k_п.

• И - интегральный (астатический):

u(t) = k_и e(t) dt, W(p) = k_и/T_иp.

• ПИ - пропорционально-интегральный (изодромный):

u(t) = k_пe(t) + (k_и/Т_и) e(t) dt, W(p) = k_п + k_и/(Т_ир).

• ПД - пропорционально-дифференциальный:

u(t) = k_пe(t) + k_дТ_и de(t)/dt, W(p) = k_п + k_дТ_др.

• ПИД - пропорционально-интегрально-дифференциальный:

u(t) = k_пe(t) + k_дТ_д de(t)/dt + (k_и/Т_и) e(t) dt, W(p) = k_п + k_дТ_др + k_и/(Т_ир).

где k_п, k_д, k_и - постоянные коэффициенты.

Задающим блоком называется блок (алгоритм), осуществляющий расчет задающего воздействия y*(t). К простейшим задающим блокам можно отнести задающие рукоятки, реостаты, пульты, генерирующие сигналы для задач стабилизации, где у* = const. В более совершенных системах это аппаратно или программно реализованные генераторы задающих сигналов.

Специальные блоки систем управления. Вспомогательные задачи определения (идентификации) неизмеряемых переменных и неизвестных параметров возникают как в САУ, так и в системах автоматического контроля. Это:

• оценивание переменных состояния объекта в условиях действия шумов (фильтрация, сглаживание, предсказание);

• идентификация параметров, оценивание неизвестных параметров системы.

Для решения перечисленных задач используются наблюдатели и идентификаторы.

Наблюдателем называется блок (алгоритм), предназначенный для оценивания переменных состояния ОУ или внешней среды. Структура наблюдателя включает в себя модель объекта управления, которая вырабатывает прогнозные текущие значения оценки y_п(t) выходной переменной y(t). Поведение модели корректируется за счет обратных связей по ошибке наблюдения (невязке)

Dy(t)= y_п(t) - y(t).

Наблюдатели применяются также в системах управления состоянием, в которых не все переменные состояния могут быть измерены или результаты измерения содержат значительные помехи.

Математическая модель (уравнение) объекта управления может содержать коэффициенты q_j - массо-инерционные, электрические, термодинамические и пр. параметры управляемого процесса и других используемых в САУ устройств. В тех случаях, когда значения параметров изменяются во времени или заранее неизвестны, появляется необходимость в использовании идентификаторов параметров.

Идентификатором называется блок (алгоритм) вида q(t)= Q(у(t), u(t), …), где Q(*) - динамический оператор, предназначенный для оценивания параметров ОУ по имеющейся информации о текущем состоянии у(t) и входном воздействии u(t) объекта, т. е. для расчета в реальном времени значений q(t). Идентификаторы применяются в адаптивных системах управления, в которых параметры регулятора не устанавливаются заранее, а настраиваются в процессе работы. В таких системах часто используются адаптивные алгоритмы управления вида u(t) = U(e(t), у*(t), q(t),...), а вектор оценки q(t) может быть получен с помощью алгоритма идентификации.

3.2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА УПРАВЛЕНИЯ [1, 8].

Математической моделью динамической системы принято называть совокупность аналитических выражений и алгоритмов, однозначно определяющих развитие процессов в системе, т. е. ее движение. В зависимости от типа сигналов различаются непрерывные и дискретные модели систем. В зависимости от используемых операторов - линейные и нелинейные, временные и частотные модели. К временным относятся модели, в которых аргументом является время (непрерывное или дискретное). Это дифференциальные и разностные уравнения, записанные в явном виде или в операторной форме. Частотные модели предусматривают использование операторов, аргументом которых является частота соответствующего сигнала.

Аналитические модели вход-выход (ВВ) - это описание связи входных и выходных сигналов динамической системы, которое применяется как для отдельных блоков, так и всей системы управления в целом. Для обозначения входных и выходных сигналов воспользуемся обозначениями, характерными для объекта управления, где входным сигналом является управляющее воздействие u(t), а выходным регулируемая переменная y(t). В этом разделе рассматриваются непрерывные временные модели, описывающие связи входных и выходных переменных динамической системы с помощью обыкновенных дифференциальных уравнений соответствующего порядка.

Система линейных уравнений объекта. В общем случае модель одноканального объекта управления описывается нелинейным дифференциальным уравнением (системой уравнений), связывающим входной сигнал управления u(t) и выходной сигнал состояния объекта y(t):

F(y', y", …, y⁽ⁿ⁾, u', u", …, u^(m)) = 0. (3.2.1)

Уравнение описывает динамическое состояние ОУ на некотором временном интервале t≥t_o, и связывает входные сигналы u(t) и их производные u⁽ⁿ⁾(t) с выходными сигналами y(t) и их производными y⁽ⁿ⁾(t). Значения у(t_o) = у_о, у'(t_o) = у'_о, ... , y⁽ⁿ⁾(t_o) = у⁽ⁿ⁾_о называются начальными значениями (условиями), а число г = n-m ≥ 1- относительной степенью модели.

Классом дифференциальных уравнений, удобным для проведения исследований, являются линейные дифференциальные уравнения. Переход к линейным дифференциальным уравнениям выполняется операцией линеаризации, при которой переменные уравнения (3.2.1) заменяются новыми переменными – отклонениями от некоторого номинального режима (y=y-y_н, u= u-u_н), начало координат переносится в точку номинального режима, а функция F раскладывается в ряд Тейлора в окрестностях этой точки по частным производным. В результате линеаризации получаем следующую систему линейных уравнений в отклонениях:

A₀(t)y⁽ⁿ⁾ + A₁(t)y^(n-1) +…+ A_n(t)y = B₀(t)u^(m) + В₁(t)y^(m-1) +…+ B_m(t)u. (3.2.2)

Порядок системы уравнений равен n по порядку производной y⁽ⁿ⁾(t), n ≥ m, так как при n < m системы технически нереализуемы. Так как все частные производные представляют собой либо постоянные матрицы, либо матрицы, зависящие только от времени, то полученное уравнение есть либо система линейных дифференциальных уравнений с постоянными коэффициентами (A_j(t) = a_j = const, B_j(t) = b_j = const), либо система с переменными коэффициентами, в зависимости от номинальной траектории.

В случае постоянных коэффициентов система называется стационарной. Как правило, входные и выходные величины объекта - скалярные функции, при этом уравнение (3.2.2) принимает вид:

a₀y⁽ⁿ⁾ + a₁y^(n-1) +…+ a_ny = b₀u^(m) + b₁y^(m-1) +…+ b_mu. (3.2.3)

где a_j, b_j – постоянные коэффициенты (параметры) модели, a₀ > 0, b₀ > 0, n - порядок модели, 0 ≤ m < n. Решение уравнений таких стационарных объектов относительно y(t) является главным объектом исследований в классической теории автоматического управления.

Система, для которой u(t)≡ 0, называется автономной. Описание автономной системы дается однородным дифференциальным уравнением вида

a₀y⁽ⁿ⁾ + a₁y^(n-1) +…+ a_ny = 0. (3.2.3')

Передаточная функция системы. Основной метод исследования линейных систем с постоянными коэффициентами - преобразование Лапласа. При нулевых начальных условиях, после преобразования Лапласа уравнения вида (3.2.3), получаем:

L[a₀y⁽ⁿ⁾ + a₁y^(n-1) +…+ a_ny] = L[b₀u^(m) + b₁y^(m-1) +…+ b_mu].

(a₀p⁽ⁿ⁾ + a₁p^(n-1) +…+ a_n)Y(p) = (b₀p^(m) + b₁p^(m-1) +…+ b_m)U(p). (3.2.4)

Y(p) = L[y(t)] = exp(-pt) y(t) dt,

U(p) = L[u(t)] = exp(-pt) u(t) dt.

Для линейного уравнения преобразование Лапласа отношения выходного сигнала Y(p) к входному сигналу U(p) при нулевых начальных условиях не зависит от самих сигналов и называется передаточной функцией системы W(p).

Y(p) = U(p) (b₀p^(m) + b₁p^(m-1) +…+ b_m) /(a₀p⁽ⁿ⁾ + a₁p^(n-1) +…+ a_n),

W(p) = (b₀p^(m) + b₁p^(m-1) +…+ b_m) /(a₀p⁽ⁿ⁾ + a₁p^(n-1) +…+ a_n), (3.2.5)

Y(p) = W(p) U(p).

Передаточная функция W(p) зависит только от самих дифференциальных уравнений и обладает свойством линейности:

Если Y(p) = Y₁(p) + Y₂(p), то U(p) = W(p)Y₁(p) + W(p)Y₂(p) = U₁(p)+U₂(p).

Если Y(p) = сY(p), то U(p) = W(p) Y(p) = с W(p) Y(p).

В общем случае замкнутая система регулирования с обратной связью рассматривается в структурной форме, приведенной на рис. 3.2.1, где используются следующие обозначения сигналов:

Y(p) = W(p)e(p); W(p) = W₁(p)W₂(p);

Y_ос(p) = W_ос(p)Y(p); e(p)=U(p)-Y_oc(p).

Рис. 3.2.1.

Выражение выходного сигнала состояния системы через входной сигнал управления:

Y(p)=W(p)(U(p)-W_ос(p)Y(p);

Y(p)(1± W(p)W_ос(p))=W(p)U(p).

Отсюда главная передаточная функция замкнутой системы:

W_зс(p) = Y(p)/U(p) = W(p)/[1 ± W(p) W_oc(p)].

Знак плюс или минус определяется типом обратной связи (отрицательная или положительная). Соответственно, выходной сигнал с учетом сигнала дестабилизирующего воздействия f(t), который суммируется с правой частью выражения (3.2.3):

Y(p)=W_зс(p)U(p) + W_f(p)f(p),

где W_f(p) – передаточная функция по возмущению. В замкнутой системе передаточная функция по возмущению определяется как отношение выходной величины, преобразованной по Лапласу, к функции возмущающего воздействия, преобразованной по Лапласу при нулевых начальных условиях. Возмущающее воздействие может быть приложено к любой точке системы.

W_f(p) = Y(p)/f(p) = W₂(p)/[1+W_oc(p)W(p)].

Передаточная функция по ошибке:

W_e(p) = e(p)/U(p) = 1/[1 + W(p) W_oc(p)].

Передаточная функция по ошибке - основное средство исследования точности САУ. C учетом возмущающего воздействия:

e(p)=W_e(p)U(p) + W_ef(p)f(p),

где W_ef(p) - передаточная функция по ошибке и возмущению (от возмущения к ошибке):

W_ef(p) = e(p)/f(p) = -W₂(p)W_oc(p)/[1 + W(p) W_oc(p)].

Передаточная функция по обратной связи:

W_Yoc(p) = Y_oc(p)/U(p) = W(p) W_oc(p)/[1 + W(p) W_oc(p)].

Типовые звенья САУ. Полиномы числителя и знаменателя передаточной функции (3.2.5) можно разложить на простейшие множители по их корням:

W(p) = N(p)/P(p) = m [(p-p₁^ч)…(p-p_m^ч)] / [(p-p₁^з)…(p-p_n^з)], (3.2.6)

где μ = b₀ /a₀ – константа, p_i^ч – множество корней числителя N(p)=0, p_i^з – множество корней знаменателя P(p)=0. Корни числителя передаточной функции называют нулями, корни знаменателя – полюсами. Комплексно сопряженные корни объединяются в квадратурные полиномы с вещественными коэффициентами: (p-α+jβ)(p-α-jβ) = p²-2αp+β²+α².

После такого представления в числителе и знаменателе будет некоторое количество скобок первого и второго порядка с вещественными числовыми коэффициентами, каждую из которых можно рассматривать, как элементарную передаточную функцию, практически реализуемую в силу вещественности коэффициентов. Если вынести из всех скобок свободные члены и объединить их произведение в общий множитель К, то получим уравнение:

W(p) = K [W₁(p)…W_z(p)], (3.2.7)

где z=n+m, если все корни вещественные, z < n+m, если есть комплексные корни. Коэффициент К принято называть коэффициентом усиления системы. Заметим, что W(0) = К = b_m/a_n, т.е. его числовое значение равно коэффициенту усиления на нулевой частоте ("постоянном токе").

Классификация звеньев производится по виду их передаточных функций, независимо от исполнения (механические, гидравлические, электрические и пр.). Передаточные функции типовых звеньев, из которых синтезируются системы, обычно имеют числитель или знаменатель, равный единице. Ниже приводятся выражения передаточных функций основных типовых звеньев систем:

1. К - Усилительное звено.

2. p - Дифференцирующее звено.

3. 1/p - Интегрирующее звено (интегратор).

4. K/(Tp+1) - Инерционное (апериодическое) звено.

5. K/(T²p+2dTp+1) - Колебательное звено.

6. K(Tp+1) - Форсирующее звено.

7. K(T²p+2dTp+1) - Форсирующее звено 2-го порядка.

Здесь Т – определенный временной коэффициент (постоянная времени). Звенья 2, 6 и 7 не реализуются в строгом теоретическом смысле, существуют только их приближения.

Типовые входные воздействия. Для оценки динамических свойств системы и отдельных звеньев принято исследовать их реакцию на типовые входные воздействия. Наиболее распространенными типовыми воздействиями являются ступенчатое, импульсное и гармоническое. Любой сигнал u(t), имеющий сложную форму, можно разложить на сумму типовых воздействий u_i(t) и на основании принципа суперпозиции получить результирующее изменение выходной величины y(t) в виде суммы реакций системы на каждую из составляющих.

Рис. 3.2.1.

Единичная ступенька.Особое значение в теории автоматического управления имеет ступенчатое воздействие 1(t) = 1 при t≥0, 1(t) = 0 при t<0 (сигнал u₁(t) на рис. 3.2.1). Все остальные воздействия могут быть сведены к нему. Так, например, импульсный сигнал может быть представлен двумя ступенчатыми сигналами одинаковой величины противоположными по знаку, поданными один за другим через интервал времени Dt(сигнал u(t) на рис. 3.2.1).

Преобразование Лапласа для единичной ступеньки:

1(p) = exp(-pt) dt = 1/p. (3.2.8)

Линейно нарастающее воздействие (t(t)=t при t≥0, t(t) = 0 при t<0) представляет собой интеграл по времени от единичной ступеньки:

t(t) = 1(t) dt, 1(t) = d t(t) /dt.

Преобразование Лапласа:

t(p) = t exp(-pt) dt = 1/p². (3.2.9)

Экспоненциальная функция exp(at). Преобразование Лапласа:

L[exp(at)] = exp(at) exp(-pt) dt = 1/(p-a). (3.2.10)

Выражение справедливо и при любом комплексном α.

Гармонические воздействия sin ωt и соs ωt.

На основе формулы Эйлера exp(jωt) = cos ωt + j sin ωt соответственно имеем cos ωt = Re exp(jωt), sin wt = Im exp(jwt). Преобразования Лапласа:

L[sin ωt] = L[Im e^jωt] = Im L[e^jωt] = Im (1/(p-jω)) = Im((p+jω)/(p²+ω²)) =

= Im(p/(p²+ω²)+jω/(p²+ω²)) = ω/(p²+ω²).

L[cos ωt] = Re L(e^jωt) = Re (1/(p-jω)) = Re((p+jω)/(p²+ω²)) = p/(p²+ω²).

Дельта - функция δ(t) - математическая модель очень короткого конечного воздействия большой мощности (единичный импульс). Определение δ(t)-функции даётся через интеграл свёртки с любой другой интегрируемой функцией x(t):

d(t-t₀) x(t) dt = x(t₀).

Отсюда, при x(t)=1:

d(t) dt = 1, d(t) exp(-pt) dt = 1, L[d(t)] = 1. (3.2.11)

Единичный импульс физически представляет собой очень узкий импульс, ширина которого стремится к нулю, а высота - к бесконечности, ограничивающий единичную площадь. Дельта - функция связана с единичной ступенчатой и линейно-нарастающей функцией выражением:

d(t) = d1(t) /dt = d² t(t) /dt².

3.3. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ САУ [7, 8].

Понятие временных характеристик. Зависимость изменения выходной величины системы от времени при подаче на ее вход единичного воздействия (импульса Дирака) при нулевых начальных условиях называется импульсным откликом системы или импульсной переходной характеристикой h(t). Эту функцию называют также функцией веса. Так как системы управления являются физически реализуемыми системами, импульсный отклик систем является односторонней каузальной функцией (h(t)=0 при t<0).

Как известно из теории сигналов и систем, отклик системы на единичный импульс определяется сверткой:

h(t) ③ d(t) = h(t) d(t-t) dt = h(t).

Выходной сигнал в каждый момент времени t_i зависит не только от входного сигнала в этот момент времени, но и от сигналов на входе во все предыдущие моменты времени t_i-t с “весом”, равным значениям функции h(t), т.е. в данном случае от сигнала d(t) при t=0.

Преобразование Лапласа свертки функций отображается произведением их изображений:

h(p) = W(p) L[d(t)] = W(p) 1 = W(p). (3.3.1)

В действительности дельта-функция в чисто теоретическом плане не реализуется. Реальные импульсные воздействия на системы всегда конечны по величине и продолжительности. Но если их продолжительность достаточно мала по сравнению со временем переходного процесса в системе (длительностью переходной характеристики в пределах заданной погрешности), то входное воздействие можно считать приближением к дельта-функции и применять для оценки переходных процессов в системе.

Не меньшее значение в САУ уделяется переходной характеристике H(t), реакции системы на единичное ступенчатое воздействие. Изображение Лапласа:

H(p) = W(p)/p. (3.3.2)

Переходная и импульсная переходная характеристики называются временными характеристиками. Каждая из них является исчерпывающей характеристикой системы и любого ее звена при нулевых начальных условиях. По ним можно однозначно определить выходную величину при произвольном входном воздействии.

Экспериментальное определение временных параметров системы и отдельных ее звеньев можно проводить подачей единичных импульсных сигналов или единичных ступеней на их входы с измерением реакции на выходах. Если на вход подать d(t) ≈ d(t) и зарегистрировать на выходе h_d(t) ≈ h(t), то изображение Лапласа передаточной функции определится выражением:

L[h_d(t)] = W_d(p) ≈ W(p).

Соответственно, при подаче на вход ступенчатой функции 1(t) регистрируется переходная функция H(t) и вычисляется W(p):

W(p) = L[dH(t)/dt].

Для произвольного входного воздействия u(t) при t≥0 переходной процесс на выходе звена при известных функциях H(t) или h(t) и нулевых начальных условиях:

y(t) = u(0)H(t) + H(t) u(t-t) dt, y(t) = h(t) u(t-t) dt.

Физическая реализуемость. Передаточная функция является физически реализуемой, если возможно создание устройства или программы, которые позволяют реально получить или вычислить выход блока с такой передаточной функцией для реальных типовых входных сигналах и их комбинаций. На выходе систем не должно появляться стремящихся к бесконечности значений сигналов в конечные моменты времени при подаче на вход конечных сигналов.

Заведомо физически нереализуемой является передаточная функция (3.2.5) с порядком числителя большим порядка знаменателя. Строго говоря, физически нереализуемой является и функция с порядком числителя равным порядку знаменателя. В первом случае после деления числителя на знаменатель выделяется, помимо прочего, несколько идеальных дифференцирующих звеньев. Во втором случае при делении числителя на знаменатель выделяется усилительное звено. Заметим, что даже идеальный усилитель не может быть физически реализован, не говоря уже об идеальном дифференцирующем звене, так как в обоих случаях частотная характеристика системы не стремятся к нулю на больших частотах.

3.4. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ САУ [7, 8, 9, 14].

Понятие частотных характеристик является важнейшим понятием, широко применяемым в теории управления. Методы, основанные на применении частотных характеристик, являются наиболее удобными в инженерной практике в классе систем с одним входом и выходом.

Функция W(jw), равная отношению выходного сигнала к входному при изменении входного сигнала по гармоническому закону, называется частотной передаточной функцией. Она может быть получена путем замены p на jw в выражении W(p). В более общей формулировке частотную передаточную функцию можно представить в виде отношения частотных спектров выходного и входного сигнала:

W(jw) = Y(jw)/U(jw) = W(p)|_p=jw.

Частотная передаточная функция линейного звена является изображением Фурье его импульсной функции и может определяться по интегральному преобразованию:

W(jw) = h(t) exp(-jwt) dt.

Для односторонних функций h(t), W(jw) есть комплексная функция, которую иногда называют амплитудно-фазо-частотной характеристикой (АФЧХ):

W(jw) = A(w) exp(jj(w)) = P(w) + jQ(w),

где P(w) - вещественная, Q(w) - мнимая частотные характеристики, А(w) - амплитудная частотная характеристика (АЧХ), j(w) - фазовая частотная характеристика (ФЧХ). АЧХ дает отношение амплитуд выходного и входного сигналов, ФЧХ - сдвиг по фазе выходной величины относительно входной:

A(w) = U_m /Y_m = |W(jw)| = ,

j(w) = arctg(Q(w)/P(w)).

Рис. 3.4.1.

Годограф, приведенный на рис. 3.4.1, является стандартным методом отображения АФЧХ на комплексной плоскости с координатами ReW(ω) и ImW(ω). Параметром на кривой годографа является частота, изменяющаяся в интервале от 0 до ∞. Для произвольной частоты ω радиус вектор в точке W(jω) показывает амплитуду выходного сигнала, а угол j(ω) - сдвиг фазы между выходным и входным сигналом. Иногда W(jω) называют комплексным коэффициентом передачи, подразумевая, что АФЧХ является обобщением обычного коэффициента усиления К на случай его зависимости от частоты и фазового сдвига, также зависящего от частоты. Комплексно сопряженные ветви АФЧХ, отличающиеся знаком j, зеркальны относительно вещественной оси.

Для частотного анализа систем применяется также раздельное построение графиков АЧХ и ФЧХ, если в том появляется необходимость.

Логарифмические частотные характеристики. В практике автоматики широкое применение находят частотные характеристики в логарифмических масштабах. Применение логарифмического масштаба позволяет наглядно изображать характеристики в большом диапазоне частот, представлять характеристики отрезками ломанных линии и определять характеристики сложных систем простым суммированием характеристик, входящих в эти системы элементов.

Частота в логарифмическом масштабе измеряется в декадах. Две частоты w₁ и w₂ отличаются на одну декаду если w₂/w₁ = 10, lg(w₂/w₁) = 1. Относительные амплитуды в логарифмическом масштабе выражаются в децибелах. Две мощности w₁ и w₂ отличаются на один децибел, если 10 lg(w₁/w₂) = 1. Так как мощности относятся как квадраты образующих их первообразных (напряжений, токов, сил и т.д.), то две первообразные a₁ и а₂ будут отличаться на один децибел, если 10 lg(а₁² /а₂²) = 1 ® 20 lg(а₁/а₂) = 1.

В CАУ широко используются логарифмические амплитудная (ЛАЧХ) и фазовая (ЛФЧХ) частотные характеристики (рис. 3.4.2). Они получаются путем логарифмирования передаточной функции:

lg[W(jw)] = lg[A(w) exp(jj(w)] = lg[A(w)]+lg[exp(jj(w)] = L(w) + j(w).

ЛАЧХ получают из первого слагаемого, которое умножается на 20, то есть L(w)=20 lg A(w). Величина L(w) откладывается по оси ординат в децибелах. Изменению сигнала в 10 раз соответствует изменение его уровня на 20 дБ. По оси абсцисс откладывается частота w в логарифмическом масштабе, единичным промежуткам по оси абсцисс соответствует изменение w в 10 раз.

Рис. 3.4.2.

ЛФЧХ, получаемая из второго слагаемого, отличается от ФЧХ только масштабом по оси w. Величина j(w) откладывается по оси ординат в градусах или радианах. Для элементарных звеньев она не выходит за пределы: -p ≤ j ≤ p.

Частотные характеристики являются исчерпывающими характеристиками системы, по которым можно восстановить ее передаточную функцию и определить параметры.

3.5. ХАРАКТЕРИСТИКИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ СИСТЕМ [1, 7, 8, 9].

Элементарными звеньями называются простейшие составные части (блоки) системы, поведение которых описывается алгебраическими уравнениями или дифференциальными уравнениями (1-2)-го порядков:

a₀ y"(t) + a₁ y'(t) + a₂ y(t) = b₀ u'(t) + b₁ u(t). (3.5.1)

Передаточная функция элементарного звена имеет вид:

W(p) = (b₀ u'(t) + b₁ u(t)) / (a₀ y"(t) + a₁ y'(t) + a₂ y(t)). (3.5.2)

Безынерционное (пропорциональное, усилительное) звено, для которого в любой момент времени выходная величина пропорциональна входной. И в статике, и в динамике описывается уравнением:

y(t) = k u(t).

Безинерционное звено передаст сигнал без искажения по форме и сдвига во времени, но измененный по амплитуде в k раз. Реальные звенья могут быть отнесены к данному типу условно, так как всегда обладают инерционностью. Однако если переходный процесс в элементах звена протекает за время, малое по сравнению с временем переходного процесса системы в целом, то эти элементы могут считаться безинерционными.

Рис. 3.5.1.

Динамический параметр k называют коэффициентом усиления. Переходная характеристика повторяет ступенчатое входное воздействие 1(t), измененное (увеличенное или уменьшенное) в k раз (рис. 3.5.1):

H(t) = k 1(t).

При k = 1 звено передает входной сигнал на выход, а при k = -1 инвертирует входной сигнал. Передаточная функция звена равна коэффициенту пропорциональности:

W(p) = k.

Функция веса представляет собой импульсную функцию, площадь которой равна k:

h(t) = k d(t).

Рис. 3.5.2.

Амплитудно-фазо-частотная характеристика АФЧХ: W(jw) = k. АЧХ: A(w) = k. ФЧХ: j(w) = 0. ЛАЧХ: L(w) = 20 lg k.

Звено пропускает все частоты одинаково c увеличением амплитуды в k раз и без сдвига по фазе (рис. 3.5.2).

Некоторые реальные звенья могут рассматриваться как безинерционные с определенной точностью (жесткий механический рычаг, механический редуктор, потенциометр, широкополосный электронный усилитель и т.п.). Многие датчики сигналов (потенциометрические, индукционные и пр.) также обычно рассматриваются как безынерционные.

Апериодическое инерционное звено первого порядка описывается дифференциальным уравнением: T dy/dt + y(t) = k u(t). Передаточная функция звена: W(p) = k/(Tp+1).

Динамические свойства определяются значениями двух величин, k и Т. Т – постоянная времени, k – коэффициент передачи (усиления) звена. Переходная функция:

H(p) = W(p) 1(p) = k/[p(Tp+1)].

При обратном преобразовании Лапласа функции Н(р) по формуле вычетов:

H(t) = k (1-exp(-t/T)

Рис. 3.5.3.

Переходный процесс инерционного звена экспоненциальный - типичный для систем первого порядка (рис. 3.5.3). Выходная величина звена в переходном режиме со скоростью, определяемой величиной Т, следует за изменением входной величины (свойство инерционности). Сигнал на выходе звена нарастает по экспоненте, поэтому звено называют апериодическим. При t→∞ сигнал стремится к значению k.

Весовая функция находится дифференцированием переходной характеристики:

h(t) = (k/T) exp(-t/T) 1(t).

Множитель 1(t) определяет существование функции при t≥0 и обычно опускается (подразумевается по умолчанию).

По переходной характеристике можно определить передаточный коэффициент k, равный установившемуся значению H(t), и постоянную времени Т по точке пересечения касательной к кривой в начале координат с ее асимптотой. Касательная при t=0 равна k/T, а при t=T значение H(t) = 0.63k. Чем больше Т, тем больше длительность переходного процесса. Практически обычно принимают, что переходной процесс заканчивается при t порядка 3T, что соответствует 95% установившегося значения. Импульсная функция h(t) также имеет касательную k/T при t=0, которая пересекает линию установившегося значения 0 в точке t=Т. Характерен скачок функции в начальный момент времени, возникающий из-за наличия на входе d-функции. Так как идеального скачка быть не может, то будет наблюдаться процесс, обозначенный на рис. 3.5.2 пунктиром.

Рис. 3.5.4.

АФЧХ инерционного звена (рис. 3.5.4):

W(jw) = k/(Tjw +1) = k(Tjw-1) /[(Tjw+1)(Tjw-1)] =

= k [1/( T²w² +1) - jTw/( T²w² +1)] =

= k exp(-j arctg Tw) / .

Годограф описывает полуокружность с наинизшей точкой на частоте w=1/Т, при этом фазовый сдвиг равен -p/4, a коэффициент усиления АЧХ равен 0.707k. При изменении частоты от 0 до ∞ радиус-вектор АЧХ монотонно убывает от значения k до 0. Полная АФЧХ для положительных и отрицательных частот представляет собой окружность.

Рис. 3.5.5а.

Пример реализации звена RC-цепочкой приведен на рис. 3.5.5а. Комплексное уравнение выходного напряжения звена в радиотехнике, определяемое законом Ома, записывается в форме:

U_вых(w) = [U_вх(jw)/(R+1/jwC)](1/jwC) = U_вх(jw)/(jwRC+1).

W(w) = U_вых(jw)/U_вх(jw) = 1/(jwRC+1).

W(w) = k/(Tp+1), где p=jw, T=RC, k=1.

Рис. 3.5.6а

На рис. 3.5.6а приведены комплексные АЧХ и ФЧХ приведенного RC-звена при Т=RC=1 и k=1 на частоте (в радианах) от -10 до 10. Как следует из этого рисунка, звено передает на выход, в основном, только низкие частоты входного сигнала (от -1/RC до 1/RC по уровню 0.707) с нарастающим подавлением высоких частот и увеличением их сдвига по фазе по мере роста частоты. Чем меньше инерционность звена (меньше Т=RC), тем больше амплитудная характеристика по своим значимым значениям вытянута по оси частот (шире полоса пропускания).

ЛАЧХ инерционного звена:

L(w) = 20 lg |W(jw)| = 20 lg k – 10 lg(T²w²+1).

Чтобы упростить использование ЛАЧХ, вводят понятие асимптотических ЛАЧХ, то есть кусочно - постоянных функций, не сильно отличающихся от истинных. Они применяются не только для инерционного звена, но и для любых более сложных передаточных функций. Переход к асимптотической ЛАЧХ выполняется в следующем порядке (рис. 3.5.5):

Выделим области низких и высоких частот, по отдельности рассмотрим поведение ЛАЧХ в этих областях и оценим максимальную ошибку, возникающую на границе областей.

В области низких частот T²ω² << 1, и можно пренебречь выражением T²ω². Получаем горизонтальную прямую: L(ω)=20lgk.

В области высоких частот T²ω² >> 1 и значением 1 можно пренебречь. Получаем уравнение прямой с наклоном 10дб./декаду в логарифмических координатах: L(ω)=20lgk - 20lgTω.

Излом асимптотической LАЧХ имеется на ω=1/T (сопрягающая частота), где ошибка максимальна, не зависит от k и T, и равна примерно -3дб.:

ΔL=20lgk-20lgk+10lg(T²ω²+1)= 10lg2 ≈ - 3.03 дб.

Уровень -3 дб. принято считать границей полосы пропускания.

Рис. 3.5.5.

ЛФЧХ асимптотически стремится к нулю при уменьшении w до нуля (чем меньше частота, тем меньше искажения сигнала по фазе) и к значению -p/2 при возрастании w до бесконечности. Перегиб кривой на сопрягающей частоте при j(w) = -p/4. ЛФЧХ всех апериодических звеньев имеют одинаковую форму и могут быть построены по типовой кривой с параллельным сдвигом вдоль оси частот.

Для всех звеньев первого порядка характерен наклон ЛАЧХ 20 дБ/дек и максимальный поворот фазы p/2.

При достаточно больших значениях Т звено на начальном участке может рассматриваться как интегрирующее, при малых Т - как безынерционное. Примеры апериодического звена: термопара, электродвигатель, четырехполюсник из сопротивления и емкости или сопротивления и индуктивности.

Интегрирующее (астатическое) звено. Идеальное интегрирующее звено описывается дифференциальным уравнением первого порядка:

dy/dt = k u(t),

Рис. 3.5.7а.

т.е. скорость изменения выходной величины пропорциональна значению входного сигнала.

Общее решение: y(t) = y(0) + k u(t) dt.

Пример реализации звена – интегрирующая емкость (рис. 3.5.7а).

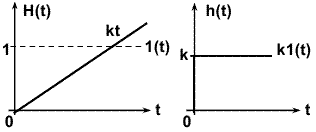Рис. 3.5.6.

Передаточная функция звена: W(p) = k/p.

Переходная характеристика при u(t) = 1(t) и нулевых начальных условиях (рис. 3.5.6):

H(t) = k 1(t) dt = kt. H(p) = k/p².

Весовая функция при u(t) = d(t) и нулевых начальных условиях (рис. 3.5.6):

h(t) = k 1(t). h(p) = k/p.

АФЧХ интегратора: W(jw) = k/jw = -jk/w = k exp(-jp/2)/w.

Рис. 3.5.7.

Интегратор ослабляет высокие частоты пропорционально частоте и неограниченно усиливает («накапливает») низкие частоты. Годограф АФЧХ (рис. 3.5.7) расположен вдоль отрицательной мнимой оси. Фазово-частотная характеристика для положительных частот имеет постоянное значение -π/2, т.е. все частоты звено пропускает с запаздыванием по фазе на 90^о. Радиус - вектор АЧХ при изменении частоты от 0 до ∞ монотонно убывает от значения ∞, стремясь к 0. Коэффициент усиления бесконечно малых частот теоретически неограничен.

ЛАЧХ интегратора:

L(w) = 20 lg |W(jw| = 20 lg k – 20 lg w.

Логарифмическая характеристика представляет собой прямую с отрицательным наклоном 20 дБ/дек, которая проходит через точку 0 дБ на частоте w = k.

При k = 1 звено представляет собой “чистый” интегратор W(p) = 1/p. Интегрирующее звено неограниченно "накапливает" входное воздействие. Примеры интегрирующих звеньев: поршневой гидравлический демпфер, электрическая емкость и т.п.

Интегрирующее звено с замедлением (рис. 3.5.8) описывается дифференциальным уравнением: T d²y(t)/dt² + dy(t)/dt = k u(t).

Передаточная функция звена: W(p) = k/[p(Tp+1)].

Рис. 3.5.8.

Для нахождения временных характеристик звена удобно представить передаточную функцию в виде суммы:

W(p) = k/p – kT/(1+Tp).

Соответственно, решение уравнения будет складываться в виде суммы решений для идеального интегрирующего звена и апериодического звена первого порядка. Переходная характеристика:

H(t) = k[t-T(1-exp(-t/T))] 1(t).

Весовая функция:

h(t) = k[1-exp(-t/T)] 1(t).

Частотные характеристики звена:

L(w) = 20 lg [k/(w )].

График асимптотической ЛАЧХ представляет собой две прямые

L1(w) = 20 lg(k) – 20 lg(w), w < 1/T,

L2(w) = 20 lg(k/T) – 40 lg(w), w > 1/T,

с отрицательными наклонами соответственно 20 и 40 дБ/дек.

Идеальное дифференцирующее звено. Выходная величина звена пропорциональна скорости изменения входной величины (производной от входной величины), а уравнение динамики имеет вид: y(t) = k du(t)/dt. Передаточная функция: W(p) = kp. При k = 1 звено осуществляет чистое дифференцирование W(p) = p.

Рис. 3.5.9.

Идеальное дифференцирующее звено реализовать невозможно, так как величина всплеска выходной величины при подаче на вход единичного ступенчатого воздействия всегда ограничена, а должна быть бесконечно большой.

Близок к идеальному звену операционный усилитель в режиме дифференцирования (рис. 3.5.9).

Переходная характеристика:

H(t) = k d1(t)/dt = k d(t),

где функция d(t) может имитироваться достаточно коротким (<<RC) импульсом с площадью, равной 1.

Импульсная характеристика:

h(t) = k dd(t)/dt.

Частотная передаточная функция:

W(jw) = kjw.

Дифференцирующее звено с замедлением. На практике используют реальные дифференцирующие звенья, осуществляющие приближенное дифференцирование входного сигнала. Реальное дифференцирующее звено является последовательным соединением двух типовых звеньев - идеального дифференцирующего kp и инерционного 1/(Tp+1). В конечном диапазоне рабочих частот характеристики такого звена могут быть сколь угодно близки к идеальным.

Звено описывается уравнением: T dy(t)/dt + y(t) = k du(t)/dt.

Передаточная функция: W(p) = kp /(Tp+1).

Рис. 3.5.10.

При малых значениях Т звено можно рассматривать как идеальное дифференцирующее.

Переходная характеристика:

H(t) = (k/T) exp(-t/T) 1(t).

Импульсная характеристика:

h(t) = [kd(t)/T – (k/T²) exp(-t/T)] 1(t).

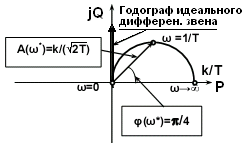Рис. 3.5.11.

По переходной характеристике, имеющей вид экспоненты (рис. 3.5.10), можно определить передаточный коэффициент k и постоянную времени Т. Примерами звеньев являются четырехполюсники из сопротивления и емкости или сопротивления и индуктивности. Дифференцирующие звенья применяются для улучшения динамических свойств САУ.

Частотная передаточная функция:

W(jw) = kjw/(jwT+1).

Годограф звена (рис. 3.5.11) описывает полуокружность с радиусом, стремящимся к бесконечности, при Т®0. При этом годограф прижимается к положительной мнимой полуоси и стремится к годографу идеального дифференцирующего звена. Частота w=1/T считается максимальной, до которой реальное звено может приниматься за близкое к идеальному.

Рис. 3.5.12.

Частотные характеристики звена приведены на рис. 3.5.12. В области высоких частот реальное звено пропускает сигнал хуже, чем идеальное. При w ® ∞ коэффициент передачи звена стремится к k/T. Фазовые сдвиги, вносимые звеном, являются наибольшими при низких частотах. На высоких частотах фазовый сдвиг стремится к нулю при w ® ∞.

Апериодическое звено второго порядка. Дифференциальное уравнение звена:

T² d²y(t)/dt² + 2rT dy(t)/dt + y(t) = k u(t),

где r - коэффициент (декремент) затухания (демпфирования). Передаточная функция:

W(p) = k/(T²p² + 2r Tp + 1).

Корни характеристического уравнения:

p_1,2 = (-r ± )/T.

Звено будет апериодическим второго порядка, если корни вещественные, или колебательным, если корни комплексные.

Если r ≥ 1, то знаменатель W(p) имеет два вещественных корня и может быть разложен на два сомножителя:

T²p²+2rTp+1 = (T₁p+1)(T₂p+1), T_1,2 = T(r ± ).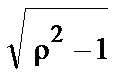

Рис. 3.5.13.

Переходная характеристика и весовая функция:

H(t) = k(1-(T₁/(T₁-T₂)) exp(-t/T₁) + (T₂/(T₁-T₂)) exp(-t/T₂)) 1(t).

h(t)