Решение

Задача 3.4

Для рамы, представленной на рисунке 3.20, необходимо:

раскрыть статическую неопределимость;

построить эпюры продольных и поперечных сил, а также изгибающих моментов;

подобрать сечение в виде двутавра,если ;

определить угол поворота сечения К.

Рисунок 3.20

Решение

1 Устанавливаем степень статической неопределимости системы. Данная система два раза статически неопределима.

2 Выбираем основную систему, удаляя «лишние связи» и заменяя исходную систему статически определимой (рис 3.21, а).

3 Получаем эквивалентную систему, загружая основную систему заданной нагрузкой и «лишними неизвестными усилиями», заменяющими действие удаленных связей (рис. 3.21, б).


а	б

Рисунок 3.21

4 Для того, чтобы определить «лишние неизвестные усилия» и , воспользуемся системой канонических уравнений:

5 Рассмотрим основную систему, нагруженную только заданной нагрузкой.

Определяем опорные реакции от действия заданной нагрузки (рис. 3.22, а).

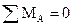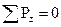Для проверки используем уравнение .

Строим эпюру изгибающих моментов от заданной нагрузки , вычисляя значения изгибающих моментов в характерных сечениях (см. рис. 3.22, а):

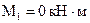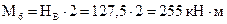
Производим построение эпюры изгибающих моментов от действия заданной нагрузки по характерным сечениям (рис. 3.22, б).


а	б

Рисунок 3.22

6 Рассмотрим основную систему, нагруженную только единичной силой .

Определяем опорные реакции от действия единичной силы (рис. 3.23, а):

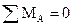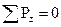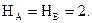
Для проверки используем уравнение .

Cтроим эпюру изгибающих моментов от единичной силы , вычисляя значения изгибающих моментов в характерных сечениях (рис. 3.23, а):

Производим построение эпюры изгибающих моментов от действия единичной силы по характерным сечениям (см. рис. 3.23, а).

7 Рассмотрим основную систему, нагруженную только единичной силой .

Определяем опорные реакции от действия единичной силой (рис. 3.23, б):

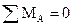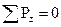Для проверки используем уравнение .

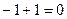Cтроим эпюру изгибающих моментов от единичной силы .

Вычисляем значения изгибающих моментов в характерных сечениях (рис. 3.23, б):

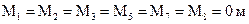Производим построение эпюры изгибающих моментов от действия единичной силы по характерным сечениям (рис. 3.23, б).


а	б

Рисунок 3.23

8 Определяем коэффициенты канонических уравнений, перемножая соответствующие эпюры, используя формулу крайних ординат:

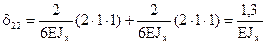9 Проверяем правильность определения коэффициентов канонических уравнений. Рассмотрим основную систему, нагруженную только единичными силами и .

Определяем опорные реакции от действия единичных сил и (рис. 3.24):

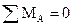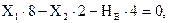
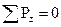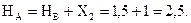
Для проверки используем уравнение .

Cтроим эпюру изгибающих моментов от единичных сил .

Вычисляем значения изгибающих моментов в характерных сечениях (рис. 3.24).

Производим построение эпюры изгибающих моментов от действия единичных сил и по характерным сечениям (см. рис. 3.24).

Рисунок 3.24

Выполняем проверку правильности определения коэффициентов , , и :

Значит, коэффициенты , , и определены верно.

Выполняем проверку правильности определения коэффициентов и :

Следовательно, коэффициенты и определены верно.

10 Решаем систему канонических уравнений:

11 Рассмотрим эквивалентную систему, т.е. статически определимую основную систему, под действием заданной нагрузки и найденных сил и (рис. 3.25, а).

Определяем опорные реакции от действия заданной нагрузки и сил и (см. рис. 3.25, а):

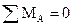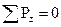Для проверки используем уравнение .

Строим окончательные эпюры внутренних силовых факторов.

Вычисляем значения продольных сил в характерных сечениях:

Вычисляем значения поперечных сил в характерных сечениях:

Вычисляем значения изгибающих моментов в характерных сечениях.

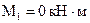Производим построение эпюр продольных сил N (рис. 3.25, б), поперечных сил Q (рис. 3.25, в), а также изгибающих моментов М_s (рис. 3.25, г) по характерным сечениям.

Так как эпюра поперечных сил пересекает базовую линию и меняет знак с «+» на «-», то в этой точке находится максимальное значение изгибающего момента. Находим положение этого сечения.


а	б

в	г

Рисунок 3.25

12 Выполняем деформационную проверку.

Так как в заданной статически неопределимой системе перемещение по направлению равно нулю, то произведение окончательной эпюры изгибающих моментов М_s на эпюру должно равняться нулю, т.е. .

При этом погрешность составила:

13 Подбираем поперечное сечение в виде двутавра.

При указанном нагружении опасным сечением является сечение 6, для которого .

Так как осевая сила незначительна, то размеры сечения подбираем из условия прочности на изгиб:

Определим требуемый момент сопротивления сечения:

Номер двутавра находим по расчетному значению момента сопротивления . По таблице сортамента (ГОСТ 8239-72) выбираем двутавр № 30, для которого , .

14 Определяем угол поворота сечения К.

Для этого к основной системе в сечении К прикладываем единичный момент, т.е. .

Определяем опорные реакции от действия единичного момента (рис. 3.26):

Вычисляем значения изгибающих моментов в характерных сечениях от действия единичного момента (см. рис. 3.26):

Производим построение эпюры изгибающих моментов от действия единичного момента по характерным сечениям (см. рис. 3.26).

Рисунок 3.26

С использованием формулы крайних ординат «перемножаем между собой» на каждом участке окончательную эпюру изгибающих моментов М_s и эпюру от действия единичного момента :

Угол поворота сечения К равен:

Допускаемый угол поворота сечения равен:

Так как угол поворота сечения К меньше, чем допускаемый угол поворота, то жесткость рамы обеспечена.