Понятие многократного измерения. Алгоритмы обработки многократных измерений.

Прямые многократные измерения и обработка их результатов. Необходимость в проведении многократных измерений некоторой физической величины x_n возникает, если в процессе измерений есть большая случайная погрешность. Задача обработки измерений заключается в нахождении наилучшей оценки измеряемой величины x_и и доверительного интервала, в котором с заданной доверительной вероятностью находится истинное значение, в соответствии с ГОСТ 8.207-76 “ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Общие положения”. Решение задачи основано на выполнении гипотезы о нормальном распределении случайных погрешностей измерений. Прямые многократные измерения делятся на равно– и неравноточные измерения. Равноточные измерения проводятся средствами измерений одинаковой точности по одной и той же методике при неизменных внешних условиях. При равноточных измерениях СКО результатов всех рядов измерений равны между собой. Проверка допустимости различия между оценками дисперсий нормально распределенных результатов измерений выполняется с помощью критерия Фишера при наличии двух групп наблюдений, и критерия Бартлета [1-3], если этих групп больше. Прямые многократные равноточные измерения и обработка их результатов. Пусть был получен ряд измерений x₁, x₂, ,x_n ,из которого исключены известные систематические погрешности. Число n зависит как от требований к точности, так и от реальной возможности проведения повторных измерений. При использовании прибора невысокой точности (в случае, когда преобладает систематическая погрешность) целесообразно ограничиться только одним измерением. Однако на практике всегда остаются некоторые неисключенные остатки систематических погрешностей. Их учет рассмотрен далее. Последовательность и этапы обработки данных: Определение точечных оценок закона распределения результатов измерений. - среднего арифметического измеряемой величины = ; - СКО результата измерений = = = ; - СКО среднего арифметического значения 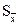= / = . Грубые погрешности исключаются. После чего повторно производится расчет. Иногда для более надежной идентификации закона распределения результатов могут определяться другие точечные оценки: коэффициент асимметрии, эксцесс и др. При числе наблюдений n<15 принадлежность полученных в эксперименте данных нормальному закону не проверяется. При числе наблюдений 15< n <50 используется составной критерий, приведенный в ГОСТ 8.207-76, а также в [1-3]. Определение доверительных границ случайной погрешности. = / − в случае использования формулы Лапласа, = / − в случае использования распределения Стьюдента. Определение границ неисключенной систематической погрешности результата измерений. Границы неисключенной систематической погрешности принимаются равными пределам допускаемых основных и дополнительных погрешностей средств измерений, если их случайные составляющие пренебрежимо малы. При наличии нескольких систематических погрешностей НСП рассчитываются по формуле: = k . На практике чаще всего задают доверительные вероятности P = 0,9 и P = 0,95. Для них коэффициенты k рекомендуется брать 0,95 и 1,1 соответственно, независимо от числа составляющих m. При доверительной вероятности P ≥ 0,99 значение k следует взять из [1-3]. Это значение зависит от числа m. Доверительная вероятность при определении границ q принимается равной доверительной вероятности, используемой при нахождении границ случайной погрешности. Определение доверительных границ погрешности результата измерения При проведении многократных измерений случайная погрешность может быть уменьшена во много раз. Погрешность усредненного результата будет определяться не зависящей от числа отсчетов систематической погрешностью.Устанавлены правила суммирования систематических и случайных погрешностей и определения границ погрешности ± . Если границы неисключенной систематической погрешности q и оценка СКО результата измерения S связаны соотношением q < 0,8 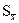, причем оценки выполнены при одинаковой доверительной вероятности, следует пренебречь систематической составляющей погрешности. Доверительные границы погрешности результата: = = / ,t_p − коэффициент Стьюдента, зависящий от доверительной вероятности Р и числа проведенных измерений. Если имеет местоq > 8 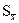, то следует пренебречь случайной составляющей, и результат характеризовать лишь границами его суммарной систематической погрешности = q. Если неравенства не выполняются, т.е. 0,8 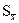< q < 8 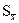, границы погрешности результата измерений определяют по формуле: = = , где = . В [2] приведена упрощенная формула расчета погрешности: = , где q − общая граница НСП, а 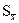− доверительная граница случайной погрешности. Погрешность расчета по такой формуле не превышает 5−10%. Запись результата измерения. Результата записывается в виде х = ± D при доверительной вероятности Р = Р_д . При отсутствии данных о функции распределения составляющих погрешности результаты измерений представляют в виде , , 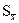n , q при доверительной вероятности Р = Р_д. Прямые многократные неравноточные измерения и обработка их результатов. Часто проводятся неравноточные измерения одной и той же физической величины: с различной точностью, либо разными приборами в различных условиях, разными исследователями и т.д. Пусть имеются m серий равноточных измерений объемом n_i , СКО серии и среднее i-й серии. Тогда [2] наиболее вероятным значением величины будет средневзвешенное: