Построение области допустимых решений целевой функции F.

Пример 2

Решить графическим способом следующую двумерную задачу линейного программирования:

Рисунок 2.3.6.

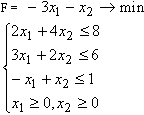
Решение:

Построение области допустимых решений целевой функции F.

Построим прямоугольную систему координат. Так как, x₁ и x₂ неотрицательны, то можно ограничится рассмотрением первого квадранта.

Рассмотрим первое ограничение:

2x₁+4x₂<=8

Заменим в данном ограничении знак неравенства знаком равенства и постоим прямую.

2x₁+4x₂=8 (1)

Найдем две точки, принадлежащие данной прямой.

x₁=0, следовательно, x₂=2: координаты (0; 2).

x₂=0, следовательно, x₁=4: координаты (4; 0)

Рассмотрим второе ограничение:

3x₁+2x₂<=6

3x₁+2x₂ =6 (2)

x₁=0,следовательно, x₂=3: координаты (0; 3).

x₂=0, следовательно, x₁=2: координаты (3; 0)

Рассмотрим третье ограничение:

x₁+x₂<=1

x₁+x₂ =1 (3)

x₁=0, следовательно, x₂=1: координаты (0; 1)

Если x₂=0, то x₁=-1, но мы рассматриваем только первый квадрант, поэтому возьмем другую точку, например, x₁=1, тогда x₂=2: координаты (1; 2)

Отложим полученные точки на числовых осях и найдем полуплоскости, которые соответствуют первым трем ограничениям (на рисунке они указаны стрелками). Заштрихованная область ОАВСD - область допустимых решений функции F.