I. Математическая модель задачи.

1) Переменные задачи. Обозначим количество туристов, которые будут перевозиться из пункта i в отель j как X_ij (i=1,2,3; j=1,2,3,4). Это переменные задачи, значения которых должны быть определены в процессе решения. Например, X₂₃ – это число туристов, которое должно быть перевезено из аэропорта (пункт 2) в отель “Слава” (пункт 3). В задаче содержится 3*4=12 переменных.

2) Ограничения на переменные задачи. Очевидно, что все переменные задачи не отрицательные и целые числа, т.е.

X_ij 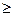0, (1)

X_ij – целые числа, (2)

где i=1, 2, 3; j=1, 2, 3, 4.

Кроме этого, должны быть удовлетворяться следующие условия. Число туристов, вывозимых с железнодорожного вокзала (пункт 1) равно 15, поэтому :

X₁₁ + X₁₂ + X₁₃ + X₁₄ = = 15 (3)

Аналогично для аэропорта (пункт 2):

X₂₁ + X₂₂ + X₂₃ + X₂₄ = = 25 (4)

И для морского вокзала (пункт 3):

X₃₁ + X₃₂ + X₃₃ + X₃₄ = = 5 (5)

По условию задачи в отеле “Морской” (пункт 1) забронировано 5 мест, поэтому:

X₁₁ + X₂₁ + X₃₁ = = 5 (6)

Аналогично, для отеля “Солнечный” (пункт 2):

X₁₂ + X₂₂ + X₃₂ = = 15 (7)

Для отеля “Слава” (пункт 3):

X₁₃ + X₂₃ + X₃₃ = = 15 (8)

Для отеля “Уютный” (пункт 4):

X₁₄ + X₂₄ + X₃₄ = 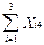= 10 (9)

Обычно транспортная задача представляется в виде таблицы, где в ячейках помещаются переменные задачи ( X_ij ), а в правом верхнем углу ячейки стоят стоимости перевозки из пункта i в пункт j ( C_ij ). В крайнем правом столбце и нижней строке таблицы записываются числа определяющие ограничения задачи (в данном примере – это число туристов в исходных пунктах и число мест в пунктах назначения – отелях).

Для примера 2 таблица имеет вид (таблица 2):

Таблица 2

Исходный пункт,i	Пункт назначения (отели),j	Число туристов в исходном пункте


	X₁₁		X₁₂	X₁₃	X₁₄

	X₂₁		X₂₂	X₂₃	X₂₄

	X₃₁		X₃₂	X₃₃	X₃₄
Число мест в отеле				å = 45 å = 45

Транспортная задача, для которой суммы чисел в последнем столбце и нижней строке равны, называется сбалансированной: 15 + 25 + 5 = 45, 5 + 15 + 15 + 10 = 45. Если транспортная задача не сбалансирована, то в таблицу добавляется еще одна строка или столбец. Причем стоимости перевозки в добавленных ячейках принимаются равными нулю.

Для нашего примера предположим, что в аэропорт прибыло не пять, а десять туристов. Сумма чисел в последнем столбце будет равна: 15 + 25 + 10 + 50. Чтобы сбалансировать задачу вводим пятый столбец (фиктивный отель) с пятью местами. Таблица в этом случае будет иметь вид ( таблица 3):

Таблица 3

Исход-ный пункт,i	Пункт назначения (отели),j	Число турис-тов в исход. пункте


	X₁₁		X₁₂	X₁₃		X₁₄	X₁₅

	X₂₁		X₂₂	X₂₃		X₂₄	X₂₅

	X₃₁		X₃₂	X₃₃		X₃₄	X₃₅
Число мест в отеле					å = 45 å = 45

3) Целевая функция. Транспортные расходы на перевозку туристов в отели вычисляются по формуле:

Z = 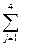C_ijX_ij = 10X₁₁ + 0X₁₂ + 20X₁₃ + ... +18X₃₄ (10)

Окончательно транспортная задача имеет вид (таблица 2). Нужно найти такие значения переменных X_ij (i=1,2,3; j=1,2,3,4) при которых целевая функция, определяемая формулой (10), будет иметь минимальное значение и будут выполнены ограничения (1) ¸ (9):

X_ij 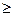0, где X_ij – целые числа (i=1,2,3; j=1,2,3,4)

;

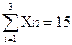
Как и в рассмотренной выше задаче распределения ресурсов (пример 1) транспортная задача является задачей линейного программирования и может быть решена симплекс-методом. В виду специфики транспортной задачи для нее был разработан специальный метод решения – метод потенциалов (см. Л1).

II. Решение транспортной задачи в процедуре EXCEL “Поиск решения”

1) Ввод данных. Вводим данные таблицы 1 и 2 в ячейки EXCEL (рис.14).

В ячейках B3 : E5 введены стоимости перевозок (табл. 1).

В ячейках F3 : F5 находится число прибывающих туристов. А в ячейках B6 : E6 находится число мест в отелях. Ячейки B8 : E10 – рабочие (изменяемые) ячейки, в которых будут вычисляться значения переменных задачи X_ij.

В ячейках F8 : F10 нужно записать формулы для вычисления левых частей ограничений (3)¸(5):

в F8 должна быть сумма ячеек B8 : E8;

в F9 должна быть сумма ячеек B9 : E9;

в F10 должна быть сумма ячеек B10 : E10.

Формулы для вычисления левых частей ограничений (6)¸(9) введем в ячейки B11 : E11:

в B11 должна быть сумма ячеек B8 : B10;

в C11 должна быть сумма ячеек C8 : C10;

в D11 должна быть сумма ячеек D8 : D10;

в E11 должна быть сумма ячеек E8 : E10;

Целевую функцию поместим в ячейку G3:

G3: СУММПРОИЗВ (B3 : E5; B8 : E10).

Таблица исходных данных имеет вид (Рис.14):

Рис.14

2) Заполнение окна процедуры «Поиск решения».

целевая функция : G3;

значение целевой функции : min;

изменяемые ячейки : B8 : E10;

ограничения задачи :

F8 : F10 = F3 : F5 (формулы (3)¸(5))

B11 : E11 = B6 : E6 (формулы (6)¸(9))

B8 : E10 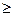0 (1) и B8 : E10 – целые числа (2)

В окне «Параметры» установить «Линейная модель», что соответствует решению задачи симплекс-методом. Результаты заполнения окна показаны на рис.15:

Рис.15

3) Выполнив процедуру «Поиск решения» получим следующие результаты (рис.16):

Рис.16

Таким образом с железнодорожного вокзала (исходный пункт 1) следует 10 туристов отвезти в отель «Уютный» (пункт 4) и 5 туристов в отель «Солнечный» (пункт назначения 2); из аэропорта (исходный пункт 2) 10 туристов отвезти в отель «Солнечный» (пункт назначения 2) и 15 туристов в отель «Слава» (пункт назначения 3); туристов прибывающих на морской вокзал (исходный пункт 3) нужно отправить в отель «Морской» (пункт назначения 1). Все эти результаты видны в конечной таблице (рис.16) При этом суммарная стоимость транспортных расходов составит 315 рублей (ячейка G3).