ЗВИЧАЙНІ ЖОРДАНОВІ ВИКЛЮЧЕННЯ (ЗЖВ)

Розглянемо систему лінійних функцій y₁, y₂, ¼, y_m від n лінійних змінних х₁, х₂, ¼, х_n у скороченому запису :

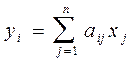
(2.1)

де змінні х_j ( j = 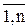) - незалежні, а y_i (і = ) - залежні.

Зобразимо цю систему у табличному вигляді:

 

	x1	x2	¼	xs	¼	xn
y1	a11	a12	¼	a1s	¼	a1n
y2	a21	a22	¼	a2s	¼	a2n			(2.2 )
¼	¼	¼	¼	¼	¼	¼
yk	ak1	ak2	¼	[aks]	¼	akn
¼	¼	¼	¼		¼	¼
ym	am1	am2	¼	ams	¼	amn

 

Таблиця (2.2 ) називається жордановою.

ЇЇ властивість: якщо елементи к-го рядка а_kj ( 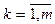) помножити на відповідні незалежні змінні х_j ( 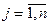) та ці добутки додати, то отримаємо залежну змінну у_к ( ).

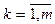Систему (2.2 ) необхідно перетворити таким чином, щоб залежна змінна у_к після перетворення стала незалежною, а незалежна змінна х_s - залежною.

Нехай у цій системі елемент а_ks ¹ 0. Із к-го рівняння знаходимо:

( 2.3 )

Змінну х_s, виражену через у_к та решту незалежних змінних (2.3 ), підставимо у решту рівнянь і зведемо подібні члени:

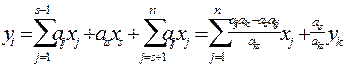i ¹ k (2.4 )

У перетвореній системі позначимо через b_ij чисельник коефіцієнта при x_j ( 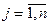) в і-му ( 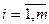) рівнянні:

b_ij = a_ij a_ks - a_is a_kj (2.5.)

Перепишемо рівняння у вигляді:

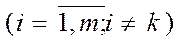(2.6)

Системи (2.4) і (2.6 ) запишемо у формі жорданової таблиці:

	х1	х2	¼	хs	¼	хn
у1	в11	в12	¼	a1s	¼	в1n	у1
у2	в21	в22	¼	a2s	¼	в2n	у2
¼	¼	¼	¼	¼	¼	¼	¼	: aks
xs	аk1	аk2	¼	[1]	¼	аkn	xs
¼	¼	¼	¼	¼	¼	¼	¼
уm	вm1	вm2	¼	ams	¼	вmn	уm

 

Наведене вище перетворення називають кроком жордановоговиключення. Перехід від жорданової таблиці (2.2 ) називають кроком ЗЖВ із розв'язувальним елементом а_{ks .}

Один крок ЗЖВ із розв¢язувальним елементом а_ks зручно розбити на такі операції:

1) розв¢язувальний елемент замінюється одиницею;

2) решта елементів розв¢язувального s-го стовпця залишається без змін;

3) решта елементів розв¢язувального к-го рядка змінюють лише знаки;

4) елементи, які не належать до розв¢язувальних рядків та стовпців, визначаються за правилом прямокутника:

b_ij = a_ij a_ks - a_is a_kj

де і, к - рядки, j,s -стовпці;

5) всі елементи нової таблиці діляться на розв¢язувальний елемент а_ks.

Якщо діагональ прямокутника, на якій міститься розв¢язувальний елемент, назвати головною, а іншу - побічною, то правило прямокутника можна с формулювати таким чином: перетворений елемент в_ij дорівнює різниці добутків елементівголовної та побічної діагоналей. Це правило залишається справедливим для розв¢язувального елемента, який розміщується в будь-якій вершині прямокутника.

Зазначимо, що коли у розв¢язувальному рядку (стовпці) є нульові елементи, то решта елементів відповідних стовпців (рядків) після одного кроку ЗЖВ залишається без змін. Це впливає з (2.5 ): при а_is= 0 або а_kj= 0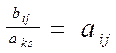

Якщо у жордановій таблиці m<=n і всі рядки лінійно незалежні, то за m послідовних кроків ЗЖВ всі залежні змінні у_і ( 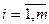) (можна перетворити на незалежні).

Приклад

Систему лінійних функцій

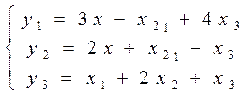
перетворити так, щоб незалежна змінна x₂ стала залежною, а залежна y₃ - незалежною.

РОЗВ¢ЯЗУВАННЯ: Запишемо систему у формі жорданової таблиці і зробимо один крок ЗЖВ з розв¢язувальним елементом а₃₂= 2

х1

х2

х3

х1

у3

х3

у1

-1

Þ

у1

-1

: 2

Þ

у2

-1

у2

-3

у3

[2]

x2

-1

-1

 

	х1	у3	х3
у1	7/2	-1/2	9/2
у2	3/2	1/2	-3/2
x2	-1/2	1/2	-1/2

 

Запишемо систему, яка відповідає останній таблиці:

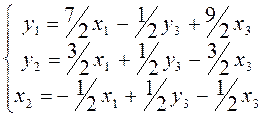
У цій системі в порівняно з вихідною незалежна змінна x₂ стала залежною, а залежна y₃ стала незалежною.