Непрерывность функции

Определение. Функция , определенная на интервале , называется непрерывной в точке , если (т.е. предел функции равен ее значению при предельном значении аргумента).

Свойства непрерывных функций:

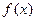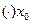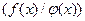1. Если функции и непрерывна в , то также непрерывны в этой точке их сумма , разность , произведение , а также частное при условии, что .

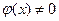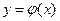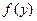2. Если функция непрерывна в точке , а функция непрерывна в точке , то сложная функция непрерывна в .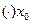

3. Функция называется непрерывной на интервале , если она на нем определена и непрерывна в каждой точке этого интервала.

4. Все элементарные функции непрерывны в соответствующей области определения.

Точки разрыва функции:

Рассмотрим функцию , определенную на интервале , кроме, быть может, точки . Значение аргумента называется точкой разрыва, если при функция определена, но не является непрерывной или не определена при этом значении . Если 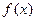имеет точку разрыва и существуют пределы слева и справа, то это точка разрыва первого рода. Если пределы справа и слева равны, то – точка устранимого разрыва. Если хотя бы один предел не существует или является бесконечным, то – разрыв второго рода.

Пример:

1. , при .

, , при 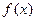неопределенна и в этой точке пределы неравны, то это разрыв первого рода.

2. , . Устранимый разрыв.

3. , , . Разрыв второго рода.

4. , . Разрыв второго рода.

5. 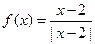. Какой разрыв в ?

. Разрыв первого рода.

6. , . Точка разрыва.

7. 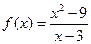(Устранимый разрыв при ).

Функция разрывна, если нарушается хотя бы одно условие: