Предел последовательности

Определение 2: бесконечной числовой последовательностью называется функция 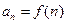, определенная для всех натуральных чисел. 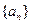– множество элементов последовательности.

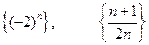– формула

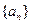Определение 2: число называется пределом числовой последовательности , если для любого существует номер , зависящий от , что для всех 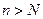выполняется неравенство .

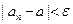или , при .

Иллюстрация .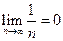

при , .

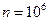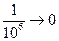Каждая числовая последовательность стремится к своему пределу по-своему.

Отметим, что последовательность может иметь только один предел. Последовательность, имеющая предел, ограничена, т.е. .

Свойства пределов:

 

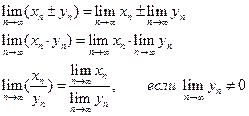
– второй замечательный предел

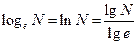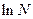( – натуральный логарифм)