УСЛОВИЯМ (ЗАДАЧА №1)

 

При решении первой задачи студентам необходимо уметь:

а) строить проекции точки по её координатам.

На оси абсцисс (рис. 3.1) от начала координат – точки О откладывают отрезок, равный X_A. Затем, через полученную точку A_X проводят перпендикулярно к оси ОХ ли-нию связи, на которой откладывают отрез-ки, равные Y_A и Z_A.

Построение проекций прямой KL вы-полняют по двум её точкам K и L. Проек-ции точек K и L строят аналогично постро-ению точки А (см. рис. 3.1);

б) анализировать положение прямой KL относительно плоскостей проекций.

Сравнивая на эпюре одноимённые проекции точек K и L, заметим, что прямая KL – прямая частного положения. В слу-чае, если Z_K=Z_L, прямая KL – горизонталь-ная, то есть прямая, параллельная плоскос-ти П₁, а если Y_K=Y_L, то прямая KL – фронтальная, то есть прямая, параллельная плоскости П₂. Для всех условий первой задачи через точку А проходит диагональ, высота или сторона плоской фигуры – то есть линия, перпендикулярная прямой KL. Следовательно, расстояние от точки А до прямой KL является исходной величиной для построения проекций плоской фигуры;

На рис. 3.2 и 3.3 показаны примеры определения расстояния от точки A до прямой KL. Эпюрное решение таких задач требует выполнения следующих действий:

1. Построим проекции перпендикуляра t к прямой KL. На основании теоремы о проецировании прямого угла, в случае, если прямая KL параллельна плоскости П₁, решение задачи начинаем с построения горизонталь-

 

ной проекции перпендикуляра (t₁ ^ K₁L₁) рис. 3.2 и (t₂ ^ K₂L₂) – в случае, если прямая KL параллельна плоскости П₂ (рис. 3.3).

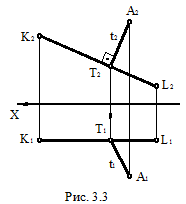
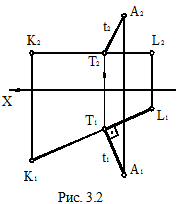
2. В том месте, где пересекается построенная проекция перпендикуляра с одноимённой проекцией прямой KL, отмечаем точку T, а далее по линии проекционной связи определяем её недостающие (на рис. 3.2 – фронтальную, а на рис. 3.3 – горизонтальную) проекции.

3. Соединяя одноимённые проекции точек A и T, получаем проекции искомого перпендикуляра AT.

Анализируя положение пря-мой AT в пространстве (см. рис. 3.2 и 3.3), приходим к выводу, что прямая AT занимает в пространстве общее положение, так как ни одна из по-строенных проекций перпендикуляра t не занимает частного положения по отношению к оси OX. Это означает, что следующим этапом решения за-дачи по определению расстояния от точки А до прямой KL должно быть «определение длины отрезка AT, перпендикулярного прямой KL». Прежде чем перейти к определению длины отрезка прямой AT, напом-ним, что его можно найти способом прямоугольного треугольника AA¢T (рис. 3.4), в котором катет │TA¢│=│A₁T₁│, так как TA¢││П₁, а катет │AA¢│ равен DZ – разности рас-

 

стояний точек A и T от плоскости П₁. Если вместо плоскости П₁ взять плоскость П₂, то длину отрезка │AT│ на фронтальной плоскости проекций можно определить, построив прямоугольный треугольник, одним из катетов которого будет фронтальная проекция A₂T₂ отрезка AT, а другим катетом – разность удалений концов отрезка AT от фронтальной плоскости проекций. Эта разность на рис. 3.5, б представлена величиной DY=Y_A – Y_T.

Примеры определения длины отрезка AT показаны на фронтальной (рис. 3.5, б) и горизонтальной (рис. 3.5, а) плоскостях проекций.

В условиях к задаче №1 длина перпендикуляра │AT│ принимается равной какой-нибудь стороне плоской фигуры или равной половине длины диагонали. Следовательно, длину отрезка │AT│ можно откладывать только на той проекции прямой KL, на которой прямая KL отображается в натуральную величину. Это построение позволит на проекции прямой KL найти проекцию одной из вершин плоской фигуры.

На рис. 3.6 показан пример построения проекций прямоугольника ABCD, с соотношением сторон AD/AB=1/2, при условии, что сторона DC принадлежит прямой KL. Вершина А и прямая KL заданы. Для решения задачи из точки А проводят перпендикуляр к прямой KL (см. рис. 3.2). Так как заданная прямая KL параллельна фронтальной плоскости проекций, то решение задачи начинают с построения фронтальной проекции A₂D₂ перпендикуляра AD. По линии проекционной связи находят горизонтальную проекцию D₁ основания перпендикуляра AD. Соединяя одноимённые проекции точек A и D, строят фронтальную A₂D₂ и горизонтальную A₁D₁ проекции перпендикуляра AD. Так как прямая AD – прямая общего положения, то длину отрезка │AD│ определяют способом прямоугольного треугольника (см. рис. 3.4 и 3.5).

 

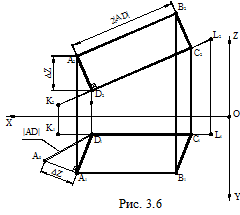Теперь, зная из условия, что большая сторона DC при-надлежит фронтальной прямой KL и вдвое больше стороны AD, то дважды откладывая длину отрезка │AD│ так, что-бы точка C была внутри отрез-ка KL, получим фронтальную проекцию C₂ точки C. По ли-нии проекционной связи и с учётом того, что точка C при-надлежит прямой KL, опреде-ляем горизонтальную проек-цию C₁ точки C (С₁ÎK₁L₁). Да-лее, исходя из свойств параллельного проецирования и свойств прямоугольника, строим фронтальную B₂, а затем горизонтальную B₁ проекции точки B.

Напомним, что если в задан-ной плоской фигуре AD и BC параллельны, то A₁D₁││B₁C₁, A₂D₂││B₂C₂; AB и DC параллельны, если A₁B₁││D₁C₁, A₂B₂││D₂C₂.

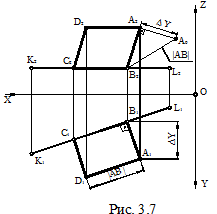
Последовательно соединив од-ноимённые проекции точек A, B, C и D, получим проекции искомой плос-кой фигуры, а именно прямоугольни-ка по заданным условиям. На рис. 3.7 показано построение проекций квад-рата, при условии, что сторона BC квадрата принадлежит прямой KL, которая расположена параллельно плоскости П₁.