Законы теплового излучения.

Одним из основных законов теплового излучения является закон Планка, который устанавливает распределение энергии теплового излучения по длинам волн для абсолютно черного тела

где С₁=0,374 10^-15[Вт м^2]- первая постоянная Планка;

С₂=1,439 10^-2 [м К] - вторая постоянная Планка;

 

 

Т - абсолютная температура тела, [К];

λ - длина волны, [м].

Зависимость спектральной интенсивности излучения абсолютно черного тела от длины волны и температуры представлена на рис.2.2. Как видно, интенсивность излучения на некоторой длине волны имеет максимальное значение. С повышением температуры этот максимум смещается в область более коротких волн. Длина волны, соответствующая максимальной интенсивности излучения, может быть получена из выражения (2.1), взяв производную от которого по λ и приравняв ее к нулю.

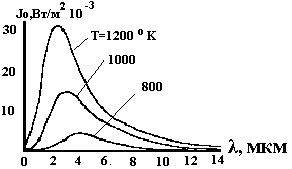
Рис.2.2. Распределение энергии излучения абсолютно

черного тела по диапазону волн.

 

Эта длина волны получается равной

Полученное выражение называется законом смещения Вина. В коротковолновой области спектра λT << С2 и в знаменателе выражения ( 2.1.) можно пренебречь единицей по сравнению с e^{( C2 / λ T )} , в результате получим приближённую формулу

J_lо = С₁ λ^-5 e^{( C2 / λ T )} , (2.1a)

которая известна как закон излучения Вина.

При λT << 0,2 С₂ [мкм ^оК] расчеты по формулам (2.1,а) и (2.1) отличаются менее 1%.

В области больших длин волн при высоких значениях температур λT >> С₂ или (С₂ / λT ) << 1, и тогда

 

 

экспоненциалъную функции в знаменателе можно разложить в ряд

e^{(С2/ λ T )}= 1+(1/1!) (С₂ / λT ) + (1/2!) (С₂ / λT )² + …

 

Ограничиваясь двумя членами ряда и подставляя их в знаменатель выражения (2.1 ) получим

J_lо = С₁ T / (С₂ λ⁴ ) . (2.1б)

Эта зависимость называется законом Релея - Джинса. Расчеты J_lо по формулам (2.1,б) и (2.1,а) при λT > 10 С₂ отличаются менее 10%.

Закон излучения Вина и закон Релея - Джинса представляют частные случаи закона Планка.

Интегральная (полная) плотность излучения абсолютно черного тела может быть получена из выражения закона Планка (2.1), интегрируя последнее по диапазону длин волн от λ = 0

до λ = ¥

E_o = ò J_lо dλ = s T ⁴, (2.2)

 

где s= 5,673 10^-8 [Bт / м² K⁴]- постоянная излучения

абсолютно черного тела.

Выражение (2.2 ) называется законом Стефана-Больцмана, который утверждает, что энергия излучения пропорциональна четвертой степени абсолютной температуры тела.

Для удобства практических расчетов выражение (2.2) записывают в несколько другом виде:

 

E_o = C_o (T/100)⁴, (2.2а)

 

где C_o = s10⁸ = 5,673 [Bт / м² K⁴] - коэффициент

излучения абсолютно черного тела.

Закон Стефана - Больцмана справедлив и для реальных тел. Для количественной оценки тепловой энергии, излучаемой реальным телом, вводится понятие степени черноты (коэффициент черноты) тела.

Под степенью черноты тела e понимается отношение

 

 

энергии, излучаемой реальным телом, к энергии, излучаемой абсолютно черным телом при той же температуре

Значение e лежит в пределах от 0 до 1 и определяется природой тела, состоянием поверхности и температурой. Для большинства материалов степень черноты увеличивается с ростом температуры, для некоторых неметаллов и покрытий наблюдается и обратная зависимость.

Кроме общей (интегральной) степени чернота e_k различают спектральную степень черноты e_l .

Спектральная степень черноты есть отношение интенсивности излучения реального тела J_l к интенсивности излучения абсолютно черного тела J_lо на той же длине волны и при той же температуре

Если реальное тело обладает непрерывным спектром излучения и e_l во всем спектре теплового излучения постоянна, то такие тела называются абсолютно серыми. Строго говоря, серых тел, так же как и абсолютно черных в природе нет. Практически многие тела могут быть отнесены к серым, при этом, чем уже рассматриваемый интервал длин волн, тем с меньшей погрешностью тело может быть отнесено к серому. В расчетах пользуются, как правило, интегральной степенью черноты, которая определяется экспериментально. Так например, для красок, эмалей, лаков e = 0,3 - 0,96, для металлов e= 0,1 - 0,8 и существенно зависит от чистоты обработки поверхности и наличия окисной пленки.

Когда известна степень черноты e, плотность излучения реального тела будет выражаться формулой

 

Связь между излучательной и поглощательной способностью тел устанавливается законом Кирхгофа, который .утверждает:

отношение излучательной способности к поглощательной для всех тел одинаково и равно излучательной способности абсолютно черного тела при той же температуре, т.е.

Из закона Кирхгофа следует:

при любой температуре излучательная способность абсолютно черного тела максимальна;

чем больше излучательная способность тела, тем больше его поглощательная способность, т.е. тела, которые хорошо излучают, хорошо и поглощают.

Из выражения (2.5) имеем Е = А Е_о, подставив Е в (2.3) получим e = А, т.е. коэффициент черноты тела равняется его коэффициенту поглощения.