Задача 2.

Дана правильная треугольная призма со стороной основания а и высотой Н. Найти расстояние между высотой основания и непересекающейся с ней апофемой боковой грани.

Решение:

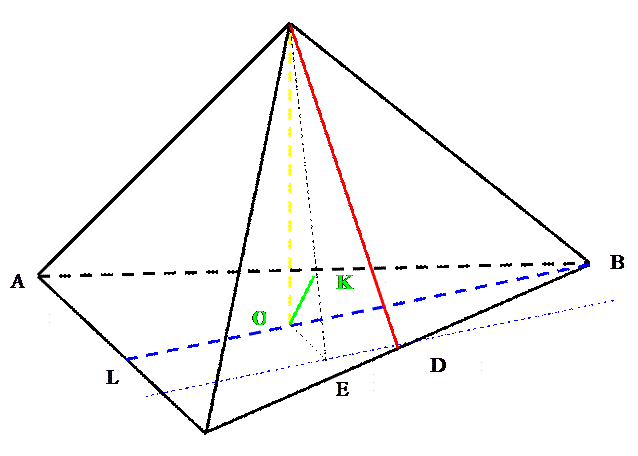
Пусть SABC – данная пирамида. Найдем расстояние между высотой основания BL и апофемой SD боковой грани SBC.

1 способ (по 1 алгоритму).

1. Через точку D проведем прямую a1 ,параллельную BL.

2. Опустим перпендикуляр SO на плоскость основания АВС.

3. Из точки О проведем перпендикуляр ОЕ к прямой а1.

4. Рассмотрим прямоугольный треугольник SOE:ОК перпендикулярно SE, ОК – искомое расстояние.

 

a

S

C

 

SO∙OE h∙a/4 a∙h

OK = −−−−− = −−−−−− = −−−−−

SE

 

 

2 способ (по 2 алгоритму)

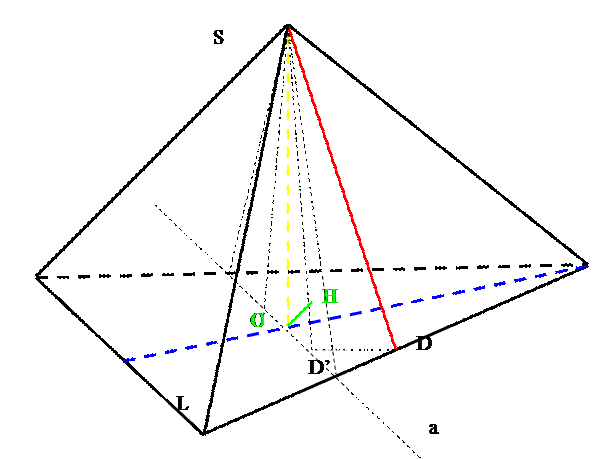
1. Из точки S восстановим перпендикуляр SO к плоскости (АВС).

2. Через точку О проведем прямую а, параллельную АС.

3. Поскольку BL перпендикулярно АС, то она перпендикулярна и а. Через точку S и прямую а построим плоскость, перпендикулярную BL.

4. Точка О – проекция BL на эту плоскость, SD’ – проекция SD на эту плоскость.

5. Из точки О опустим перпендикуляр на SD’, OH – искомое расстояние.

 

B

C

A

 

 

OH находится из треугольника SOD’ так же, как в 1 случае.