Окружность

Уравнение окружности с центром в точке и радиусом имеет вид

. (1)

Это – каноническое уравнение окружности.

Уравнение второй степени относительно текущих координат x и y является уравнением окружности тогда и только тогда, когда в этом уравнении коэффициенты при квадратах координат равны, а член с произведением координат отсутствует. Таким образом, это уравнение имеет вид

(2)

Задача.Определить координаты центра и радиус окружности, заданной общим уравнением

Решение. Приведем данное уравнение к виду (1). Для этого разделим все его члены на 9, а затем сгруппируем отдельно члены, содержащие x и y:

Дополним выражения, стоящие в каждой из скобок, до полного квадрата:

;

Теперь данное уравнение принимает вид

Или

Откуда

Сравнивая это уравнение с уравнением (1), получим , 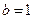и . Таким образом, данная окружность имеет центр в точке и радиус .

Эллипс

Эллипс есть множество точек, сумма расстояний которых от двух фиксированных точек, называемых фокусами эллипса, есть величина постоянная , большая чем расстояние между фокусами .

В₂

Уравнение эллипса имеет вид

, (1)

Где .

А₁А₂=2а – большая ось

В₁В₂=2в – малая ось

F₁F₂=2c – фокусное расстояние

Эксцентриситетом эллипса называется отношение расстояния между фокусами к его большой оси, т.е.

. (2)

Очевидно, что .

Если эллипс, определяемый уравнением вида (1), расположен так, что его фокусы лежат на оси , то тогда и большой осью служит отрезок длиной , а малой осью – отрезок длиной . Эксцентриситет такого эллипса вычисляется по формуле

Где .

Задача.Найти оси, вершины, фокусы и эксцентриситет эллипса

Решение. Приведем данное уравнение к простейшему виду (1), для чего свободный член перенесем вправо и разделим на него все члены уравнения. В результате получим

, или .

Сравнивая полученное уравнение с уравнением (1), имеем , . Отсюда находим оси эллипса , и координаты вершин , , , . Далее, находим .

Следовательно, фокусами эллипса служат точки и . Эксцентриситет эллипса вычисляем по формуле (2): .

Задача.Показать, что уравнение

Представляет собой уравнение эллипса.

Решение. Приведем данное уравнение к простейшему виду. Для этого сгруппируем отдельно члены, содержащие переменные и :

В каждой из скобок вынесем коэффициент при квадрате переменной, а затем выделим полный квадрат:

;

Данное уравнение преобразуем теперь к виду

Или

Откуда

Гипербола

Стр. 47.

Гиперболой называется множество точек, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная

, меньшая, чем расстояние между фокусами

Стр. 47.

Уравнение гиперболы имеет вид

, (1)

Где .

А₁А₂=2а – действительная ось

В₁В₂=2в – мнимая ось

F₁F₂=2c – фокусное расстояние

Эксцентриситетом гиперболы называется отношение расстояния между фокусами к ее действительной оси:

. (2)

Очевидно, что .

Гипербола имеет две асимптоты, уравнения которых

и . (3)

Если мнимая ось гиперболы направлена по оси 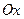и имеет длину , а действительная ось длиной направлена по оси , то уравнение гиперболы имеет вид

. (4)

Эксцентриситет такой гиперболы вычисляется по формуле

Её асимптоты те же, что и у гиперболы (1).

Задача.Найти оси, вершины, фокусы, эксцентриситет и уравнения асимптот гиперболы

Решение. Перенесём свободный член вправо и разделим на него все члены данного уравнения. В результате получим простейшее уравнение гиперболы

, или .

Сравнивая это уравнение с уравнением (1), имеем , . Таким образом, действительная ось гиперболы , а мнимая ось ; координаты вершин и . Далее, ; следовательно, фокусами гиперболы служат точки и . Эксцентриситет гиперболы вычисляем по формуле (2): . Наконец, подставляя значения , в формулы (3), получаем уравнения асимптот гиперболы: и .

Задача.Показать, что уравнение

Представляет собой уравнение гиперболы.

Решение. Приведём данное уравнение к простейшему виду (ср. с решением задачи 3.46):

;

; .