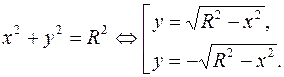II Параметрическое задание линии

Определение 3. Если абсцисса и ордината произвольной точки линии заданы как функции некоторой вспомогательной переменной, а именно:

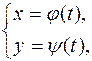(3)

то говорят, что линия задана параметрически. Уравнения (3) называют параметрическими, переменную t – параметром.

Параметрическое представление линии естественно возникает, если эту линию рассматривать как траекторию движения материальной точки, непрерывно движущейся по определенному закону.

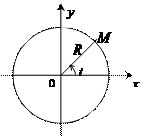
В качестве примера установим параметрические уравнения окружности радиуса R с центром в начале координат. Пусть M(x,y) – текущая точка окружности, а t – угол между радиус-вектором этой точки и осью Ox, отсчитываемый в положительном направлении. Вспоминая определение синуса и косинуса произвольного угла, нетрудно получить

 

 

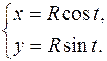(4)

Это и есть параметрические уравнения рассматриваемой окружности. Параметр может принимать любые значения, но для того, чтобы точка M(x,y) один раз обошла окружность, следует ограничить область измерения параметра, например, промежутком 0≤t<2π.

Замечание 3. Иногда удается из параметрических уравнений исключить параметр и прийти к уравнению вида F(x,y)=0. Например, если уравнения (4) возвести в квадрат и сложить, то получим известное уравнение рассматриваемой окружности: x²+y²=R².

Замечание 4. Часто линию L определяют не уравнением вида F(x,y)=0, а разрешенным относительно какой-либо переменной, например уравнением y=f(x). В таком случае говорят, что линия задана явно, линия является графиком функции. Заметим, что такой способ задания является частным случаем параметрического:

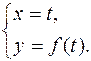
Иногда одно уравнение вида F(x,y)=0 распадается на несколько явных: