I Две задачи аналитической геометрии.

Уравнение линии на плоскости

Буквами x,у,t,s,… будем обозначать переменные величины, а записью F(x,y) или F(t,s) – любое выражение с переменными, например:

x²+y²–25=0, x²–4=0 (одна переменная x – это частный случай двух переменных).

Говорят, что числа x=x₀ и y=y₀ удовлетворяют уравнению F(x,y)=0, если при подстановке их в это уравнение вместо переменных оно становится верным числовым равенством. Например, x=4 и y=5 удовлетворяют уравнению x²+y²–25=0, а числа x=1 и y=3 этому уравнению не удовлетворяют. Конечно, среди множества уравнений встречаются такие, которым не удовлетворяют ни какие пары чисел (например, x²+y²+1=0) и такие, которым удовлетворяют любые пары значений переменных (например, 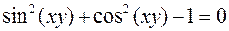). Мы исключим из рассмотрения эти крайности.

Кроме букв, обозначающих переменные, уравнение может содержать также и другие символы a, b, c,… которые представляют собой фиксированные (хотя бы и не указанные) числа. Их принято называть параметрами уравнения. Например, в уравнении ax+by–9=0 параметрами являются а и b.

Пусть на плоскость задана некоторая ДПСК и некоторая линия L. Пару чисел (x,y) мы интерпретируем как точку плоскости.

Определение 1. Уравнением данной линии L называется такое уравнение с двумя переменными F(x,y)=0, которому удовлетворяют координаты x и y любой точки, лежащей на линии L, и не удовлетворяют координаты ни одной точки, не лежащей на L.

С этим определением связана одна из задач аналитической геометрии на плоскости: по геометрическому (словесному) определению линии составить (говорят “вывести”) её уравнение. Здесь возможны две ситуации:

1) система координат дана; например, составить уравнение линии, все точки которой равноудалены от точек A(1;0) и В(0;1);

2) система координат не дана, требуется вначале выбрать её; например, составить уравнение линии, все точки которой равноудалены от двух окружностей, имеющих внешнее касание.

Очевидно, что во втором случае уравнение линии будет зависеть от выбранной системы координат.

Пример. Вывести уравнение линии, все точки которой находятся вдвое ближе от точки А(2;0), чем от точки B(8;0).

Решение. Это типовая задача и мы решим её по определенной схеме.

1. Обозначим буквой М произвольную точку линии (говорят “текущую точку”), т.е. точку с переменными координатами x и y (“текущие координаты”).

2. Условие, характеризующее все точки линии, запишем в математических символах:

. (1)

3. Выясним в последнем соотношении все величины, которые могут меняться при произвольных движениях точки M. Ими являются оба расстояния.

4. Выразим указанные величины через текущие координаты точки M и заменим их в соотношении (1) этими выражениями. Имеем:

.

Отсюда и из (1) находим:

. (2)

Это и есть искомое уравнение, ему удовлетворяют координаты любой точки, рассматриваемой линии, и не удовлетворяют координаты никакой другой точки плоскости. Задача решена. Мы можем только пожелать упростить уравнение (2). С этой целью возведем обе части в квадрат, раскроем скобки и приведём подобные. В результате получим

x²+y²=16.

Замечание 1. В общем случае при возведении обеих частей уравнения в квадрат можем получить уравнение, не равносильное исходному. В нашем случае этого не произошло, ибо обе части уравнения (2) положительны.

Во многих задачах уравнение линии играет роль первичного данного, а сама линия рассматривается, как нечто вторичное.

Определение 2. Линия, определяемая данным уравнением вида F(x,y)=0, есть геометрическое место точек, координаты которых удовлетворяют этому уравнению.

Вторая задача аналитической геометрии состоит в том, чтобы по данному уравнению изучить свойства линии, построить её.

Пример. Выяснить, какую линию определяет уравнение x²–y²=0.

Решение. Запишем уравнение в виде (x–y)(x+y)=0, что равносильно совокупности уравнений

Первое из них определяет биссектрису первой и третьей четверти, а второе – биссектрису второй и четвертой четверти. Итак, исходное уравнение определяет биссектрисы координатных углов.

Замечание 2. Конечно, существуют уравнения, которые либо вообще не определяют никакого геометрического образа (x²+y²+1=0), либо определяют геометрический образ, отличный от того, что мы привыкли понимать под словом “линия”. Например, уравнение x²+y²=0 определяет лишь одну точку (0;0), а уравнение определяет первый и третий квадранты.

В дальнейшем вместо выражения “дано уравнение линии F(x,y)=0” будем говорить короче: “дана линия F(x,y)=0”.